搜索
【题目】在平行四边形ABCD中,对角线AC、BD交于一点O,AB=11cm,△OCD的周长为27cm,则AC+BD=_____________cm.
参考答案：
【答案】32
【解析】
首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为27，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和．
∵四边形ABCD是平行四边形，
∴AB=CD=11cm，OA=OC，OB=OD，
∵△OCD的周长为27cm，
∴OD+OC=2711=16cm，
∵BD=2DO，AC=2OC，
∴BD+AC=2(OD+OC)=32cm，
故答案为：32.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线y＝（k﹣2）x+k经过第一、二、四象限，则k的取值范围是（ ）
A.k≠2B.k＞2C.0＜k＜2D.0≤k＜2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以△ABC的一边AB为直径的半圆与其它两边AC，BC的交点分别为D、E，且
=
．
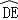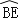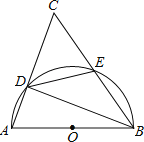
（1）试判断△ABC的形状，并说明理由．
（2）已知半圆的半径为5，BC=12，求sin∠ABD的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=﹣x2+bx+C的图象过点A（﹣3，0），C（0，3）．
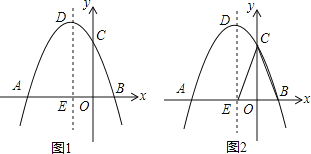
（1）求抛物线的解析式；
（2）探究：在抛物线的对称轴DE上是否存在点P，使得点P到直线AD和到x轴的距离相等？若存在，求出点P的坐标；若不存在，请说明理由；
（3）探究：在对称轴DE左侧的抛物线上是否存在点F，使得2S△FBC=3S△EBC？若存在，求出点F的坐标；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景
已知在△ABC中，AB边上的动点D由A向B运动（与A、B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于点F，点H是线段AF上一点．
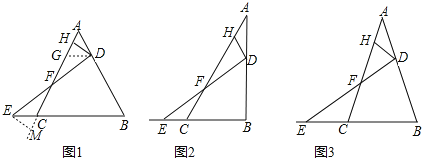
（1）初步尝试
如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等．求证：HF=AH+CF．
小王同学发现可以由以下两种思路解决问题：
思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立；
思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立．
请你任选一种思路，完整地书写本小题的证明过程（如用两种方法作答，则以第一种方法评分）；
（2）类比探究
如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是
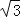：1，求
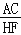的值；（3）延伸拓展
如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记
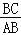=m，且点D，E的运动速度相等，试用含m的代数式表示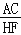（直接写出结果，不必写解答过程）． -
科目： 来源： 题型：
查看答案和解析>>【题目】楼顶所在高度为18米，此时气球在楼顶正上方5米处，则气球的高度为___________米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=kx+b与反比例函数y=
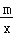的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点D．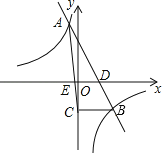
（1）求一次函数与反比例函数的表达式；
（2）过点B作BC⊥y轴，垂足为C，连接AC交x轴于点E，求△AED的面积S．
相关试题
