Question

【题目】如图，抛物线y=ax2+bx+2与坐标轴交于A、B、C三点，其中B（4，0）、C（﹣2，0），连接AB、AC，在第一象限内的抛物线上有一动点D，过D作DE⊥x轴，垂足为E，交AB于点F．

（1）求此抛物线的解析式；
（2）在DE上作点G，使G点与D点关于F点对称，以G为圆心，GD为半径作圆，当⊙G与其中一条坐标轴相切时，求G点的横坐标；
（3）过D点作直线DH∥AC交AB于H，当△DHF的面积最大时，在抛物线和直线AB上分别取M、N两点，并使D、H、M、N四点组成平行四边形，请你直接写出符合要求的M、N两点的横坐标．

Answer 1

【答案】
（1）

【解答】解：∵B，C两点在抛物线y=ax2+bx+2上，

∴，

解得：．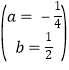

∴所求的抛物线为：y=．

（2）

抛物线y=，则点A的坐标为（0，2），

设直线AB的解析式为y=kx+b，

∴，

解得：．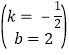

∴直线AB的解析式为y=x+2，

设F点的坐标为（x，x+2），则D点的坐标为（x，），

∵G点与D点关于F点对称，

∴G点的坐标为（x，），

若以G为圆心，GD为半径作圆，使得⊙G与其中一条坐标轴相切，

①若⊙G与x轴相切则必须由DG=GE，

即，

解得：x=，x=4（舍去）；

②若⊙G与y轴相切则必须由DG=OE，

即

解得：x=2，x=0（舍去）．

综上，以G为圆心，GD为半径作圆，当⊙G与其中一条坐标轴相切时，G点的横坐标为2或．

（3）

M点的横坐标为2±，N点的横坐标为±．

【解析】（1）根据B，C两点在抛物线y=ax2+bx+2上，代入抛物线得到方程组，求出a，b的值，即可解答；
（2）先求出直线AB的解析式为y=﹣x+2，设F点的坐标为（x，-x+2），则D点的坐标为（x，），根据G点与D点关于F点对称，所以G点的坐标为（x，），若以G为圆心，GD为半径作圆，使得⊙G与其中一条坐标轴相切，分两种情况解答：①若⊙G与x轴相切则必须由DG=GE；②若⊙G与y轴相切则必须由DG=OE；
（3）M点的横坐标为2±2，N点的横坐标为±2．