【题目】抛物线y=x2﹣4x+3与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点C在反比例函数![]() (k≠0)的图象上,求反比例函数的解析式.
(k≠0)的图象上,求反比例函数的解析式.
参考答案:
【答案】
(1)
【解答】解:令y=0,得到x2﹣4x+3=0,即(x﹣1)(x﹣3)=0,
解得:x=1或3,
则A(1,0),B(3,0),
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点C的坐标为(2,﹣1);
(2)
∵点C(2,﹣1)在反比例函数![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=﹣1×2=﹣2,
∴反比例函数的解析式为![]() ;
;
【解析】(1)令抛物线解析式中y=0得到关于x的方程,求出方程的解得到x的值,确定出A与B坐标即可;配方后求出C坐标即可;
(2)将求得的点C的坐标代入反比例函数的解析式即可求得k值.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.

(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=
 ,下列说法错误的是( )
,下列说法错误的是( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.
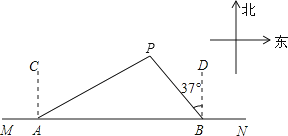
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.

(1)求证:BC是⊙O的切线;
(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC= ,AD=3,求直径AB的长.
,AD=3,求直径AB的长.
相关试题

