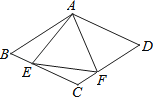
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是____.
参考答案:
【答案】![]()
【解析】解:如图,连接AC,∵四边形ABCD为菱形,∠BAD=120°,∠1+∠EAC=60°,∠3+∠EAC=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=60°,∴△ABC和△ACD为等边三角形,∴∠4=60°,AC=AB.
在△ABE和△ACF中,∵∠1=∠3,AC=AC,∠ABC=∠4,∴△ABE≌△ACF(ASA),∴S△ABE=S△ACF,∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,作AH⊥BC于H点,则BH=2,∴S四边形AECF=S△ABC=![]() BCAH=
BCAH=![]() BC
BC![]() =
=![]() ,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短,∴△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又∵S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大,∴S△CEF=S四边形AECF﹣S△AEF=
,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短,∴△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又∵S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大,∴S△CEF=S四边形AECF﹣S△AEF=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=
 x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )
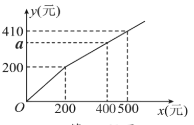
A.300B.320C.340D.360
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为__.

-
科目: 来源: 题型:
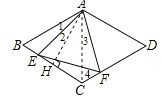
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD
BD其中正确结论的为______(请将所有正确的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

相关试题

