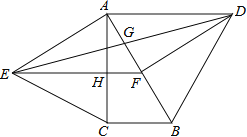
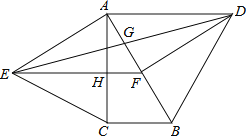
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

参考答案:
【答案】①③④
【解析】试题分析:根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形而不是菱形,根据平行四边形的性质得出AD=4AG,从而得到答案.
解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF=![]() BC,
BC,
∵BC=![]() AB,AB=BD,
AB,AB=BD,
∴HF=![]() BD,故④说法正确;
BD,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG=![]() AF,
AF,
∴AG=![]() AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=8,an=2,则am﹣n的值等于( )
A.3B.4C.8D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1)、B(-1,-1)、C(1,-1)、D(1,1)四点组成的正方形边线(如图①所示)按一定方向运动.图②是点P运动的路程s(个单位)与运动时间£(秒)之间的函数图象,图③是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.

(1)s与t之间的函数关系式是_______.
(2)与图③相对应的点P的运动路径是_______;点P出发______秒首次到达点B处.
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:0.252019×(﹣4)2020=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直平分且相等的四边形是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】直棱柱的侧面都是( )
A.正方形
B.长方形
C.五边形
D.菱形
相关试题

