【题目】如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行几米?
参考答案:
【答案】解:如图,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,则四边形EBDC是矩形,连接AC,
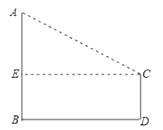
∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,
在Rt△AEC中,AC= ![]() =10m,
=10m,
答:一只鸟从一颗树的树梢飞到另一颗树的树梢,小鸟至少飞行10m.
【解析】根据题意抽象出几何图形,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,根据矩形的判定得出四边形EBDC是矩形 ,根据矩形的性质得出EB=4m,EC=8m ,从而得出AE的长,在Rt△AEC中,利用勾股定理算出AC的长,即知道了小鸟飞行的最短距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为
 ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角都等于36°,那么它是( )
A. 正六边形 B. 正八边形 C. 正十边形 D. 正十二边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图。在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.

(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
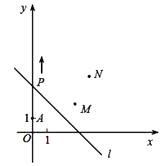
(1)当t=3时,求l的解析式;
(2)若点M , N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣a﹣1=0,则a3﹣2a+2011=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a+b=8,a2-b2=24,那么a-b=______.
相关试题

