【题目】如图1所示,在平面直角坐标系中,![]() 、
、![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足关系式
满足关系式![]() ,平移
,平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() .
.
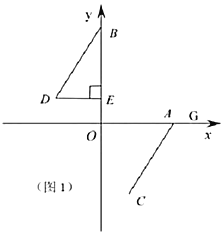
(1)直接写出![]() 、
、![]() 两点的坐标,则
两点的坐标,则![]() (______,______)、
(______,______)、![]() (______,______).
(______,______).
(2)如图1,过点![]() 作
作![]() 轴交于
轴交于![]() 点,猜想
点,猜想![]() 与
与![]() 数量关系,并说明理由.
数量关系,并说明理由.
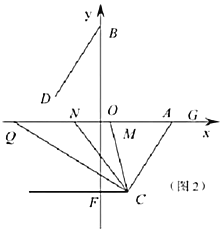
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 点,
点,![]() 为
为![]() 轴上点
轴上点![]() 左侧的一动点,连接
左侧的一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
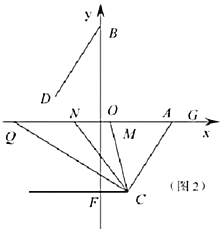
参考答案:
【答案】(1)3;0;-2;1;(2)互补,理由见解析;(3)不变;![]() .
.
【解析】
(1)根据算术平方根的非负性和平方的非负性即可求出a、b的值,从而求出A、B的坐标,再根据A、B的坐标即可发现点A到点B的平移规律,从而得到:点C到点D的平移规律,即可求出D点坐标;
(2)延长DE和CA交于点P,根据平行线的性质即可证出:![]() =∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:
=∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:![]() 与
与![]() 互补;
互补;
(3)根据角平分线的定义可得:∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,从而得出∠MCN=∠ACN-∠ACM=
,从而得出∠MCN=∠ACN-∠ACM=![]() ,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出
,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出![]() 的值.
的值.
解:(1)∵![]()
∴![]()
解得:![]()
∴点A坐标为:(3,0),点B的坐标为:(0,4)
∵平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,
,
由坐标可知:点A到点B的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点C到点D的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点D的坐标为:(1-3,﹣3+4)=(-2,1);
(2)互补,理由如下,
延长DE和CA交于点P,如下图所示
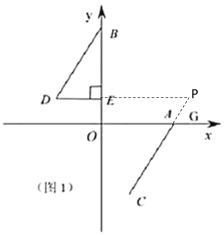
∵BD∥CA
∴![]() =∠P
=∠P
∵DE⊥y轴
∴DE∥x轴
∴![]() =∠P=∠OAC
=∠P=∠OAC
∵∠OAC+∠CAG=180°
∴![]() +∠CAG=180°
+∠CAG=180°
∴![]() 与
与![]() 互补;
互补;
(3)不变,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,
,
∴∠MCN=∠ACN-∠ACM=![]() -
-![]() =
=![]() =
=![]() ,
,
∵![]() 轴,
轴,
∴∠AQC=∠FCQ,
∴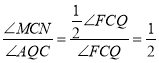 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

-
科目: 来源: 题型:
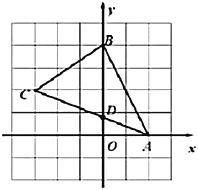
查看答案和解析>>【题目】在平面直角坐标系中,
 的顶点坐标分别为
的顶点坐标分别为 ,
, ,
, .
.
(1)求
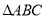 的面积.
的面积.(2)若
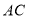 交
交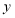 轴于点
轴于点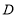 ,请求出
,请求出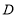 点的坐标.
点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将如图1中的边长为1个单位长度的10个小正方形,沿
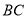 、
、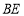 剪开,后把阴影部分补到如图2三角形
剪开,后把阴影部分补到如图2三角形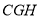 与三角形
与三角形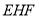 位置中,拼成了一个大正方形,大正方形的边长设为
位置中,拼成了一个大正方形,大正方形的边长设为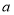 ;如图3将直径为1的圆放在点
;如图3将直径为1的圆放在点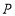 处,
处,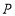 对应的数位
对应的数位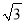 ,将圆周沿数轴向左边滚动一周到
,将圆周沿数轴向左边滚动一周到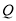 点,
点,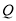 对应数为
对应数为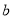 ,请完成下面问题:
,请完成下面问题: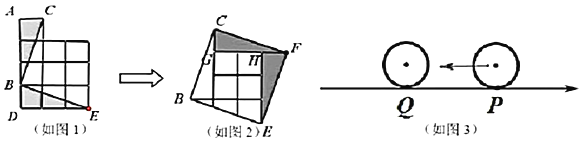
(1)求出
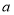 与
与 的值.
的值.(2)化简求值:
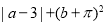
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点P(m,4)在反比例函数y=
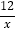 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).(1)求正比例函数的解析式;
(2)在x轴上求一点M,使△MPQ的面积等于18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,左右两幅图案关于y轴对称,右图案中的左右眼睛的坐标分别是(2,3),(4,3),嘴角左右端点的坐标分别是(2,1),(4,1).
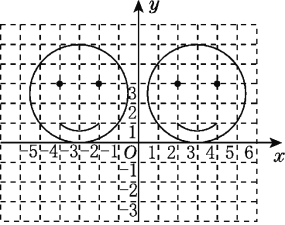
(1)试确定左图案中的左右眼睛和嘴角左右端点的坐标;
(2)从对称的角度来考虑,说一说你是怎样得到的;
(3)直接写出右图案中的嘴角左右端点关于原点的对称点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
(3)若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a<20),问该商场该如何进货,才能获得最大的利润?
相关试题

