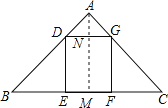
【题目】如图1,在△ABC中,AB=AC=5,BC=6,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上.
(1)求正方形DEFG的边长;
(2)如图2,在BC边上放两个小正方形DEFG、FGMN,则DE= .

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)过点作AM⊥BC于点M,由AB=AC=10,BC=16,根据等腰三角形的性质与勾股定理,即可求得AM的长,又由四边形DEFG是矩形,易证得△ADG∽△ABC,设MN=DE=x,由相似三角形对应高的比等于相似比,即可得方程![]() ,则可表示出DG的长,由正方形的性质可得DE=DG,可得结果;
,则可表示出DG的长,由正方形的性质可得DE=DG,可得结果;
(2)由题意得:DN=2DE,由(1)知:![]() ,即可得到结论.
,即可得到结论.
解:过点作AM⊥BC于点M,
∵AB=AC=5,BC=6,
∴BM=![]() BC=3,
BC=3,
在Rt△ABM中,AM=![]() =4,
=4,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE,
设MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴![]() ,
,
解得:DG=﹣![]() x+6,
x+6,
∵四边形DEFG为正方形,
∴DE=DG,即x=﹣![]() x+6,
x+6,
解得x=![]() ,
,
∴正方形DEFG的边长为![]() ;
;
(2)由题意得:DN=2DE,
由(1)知:![]() ,
,
∴DE=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∣a-2∣+b2-2b+1=0,则a2-b=_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a+b=-3,ab=2,求下列各式的值:
(1)a2b+ab2;(2)a2+b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在13×13的网格图中,已知△ABC和点M(1,2).
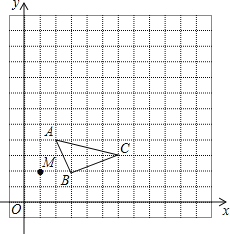
(1)以点M为位似中心,位似比为2,画出△ABC放大后的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标;
(3)若点P(a,b)在△ABC内,则点P的对应点P′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和与外角和相等,则它是_______边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:(1)a<O;(2)b2﹣4ac<0;(3)b>O;(4)a+b+c>0;(5)a﹣b+c>0.你认为其中正确信息的个数有( )

A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=3厘米,AD=4厘米,点P以每秒
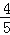 厘米的速度在BC上从B往C运动,同时点Q以每秒1厘米的速度在CA上从C往A运动,设运动时间为t秒.
厘米的速度在BC上从B往C运动,同时点Q以每秒1厘米的速度在CA上从C往A运动,设运动时间为t秒.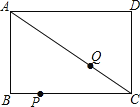
(1)当PQ平行于AB时,求t的值;
(2)是否存在某一时刻t,使点P、Q、D三点在同一直线上?若存在,求出t;若不存在,请说明理由;
(3)当△PQC为等腰三角形时,求t的值.
相关试题

