Question

【题目】在矩形ABCD中，AB=3厘米，AD=4厘米，点P以每秒厘米的速度在BC上从B往C运动，同时点Q以每秒1厘米的速度在CA上从C往A运动，设运动时间为t秒．

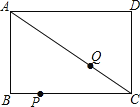
（1）当PQ平行于AB时，求t的值；

（2）是否存在某一时刻t，使点P、Q、D三点在同一直线上？若存在，求出t；若不存在，请说明理由；

（3）当△PQC为等腰三角形时，求t的值．

Answer 1

【答案】（1）t=；（2）当t=时，点P、Q、D三点在同一直线上；（3）t=或t=或t=时，△PQC为等腰三角形．

【解析】

试题分析：（1）根据勾股定理求出AC的长，根据平行线分线段成比例定理列出比例式，计算即可；

（2）根据相似三角形的性质得到=，代入数据计算即可；

（3）分CQ=CP、QP=QC、PQ=PC三种情况，根据等腰三角形的性质和相似三角形的性质进行计算即可．

解：（1）∵∠B=90°，AB=3厘米，AD=4厘米，

∴AC==5厘米，

由题意得，BP=t，CQ=t，则CP=4﹣t，

∵PQ∥AB，

∴=，即=，

解得t=；

（2）∵四边形ABCD为矩形，

∴AD∥BC，

如图2，当点P、Q、D三点在同一直线上时，=，即=，

解得t1=（舍去），t2=，

则当t=时，点P、Q、D三点在同一直线上；

（3）当CQ=CP时，4﹣t=t，

解得t=；

当QP=QC时，

如图3，作QE⊥BC于E，

则PE=EC=（4﹣t），

∵QE∥AB，

∴=，

即=，

解得t=；

当PQ=PC时，

如图4，作PF⊥AC于F，

则FC=QC=t，

∵PF⊥AC，∠B=90°，

∴△CFP∽△CBA，

∴=，即=，

解得t=，

综上所述，t=或t=或t=时，△PQC为等腰三角形．