搜索
【题目】一个多边形的内角和与外角和的和是1440°，通过计算说明它是几边形
参考答案：
【答案】八边形；证明见解析.
【解析】
设它是n边形，根据多边形的内角和公式及外角和为360°列出方程，解方程即可.
设它是n边形，依题意得：
（n-2）×180°+360°=1440°．
解得：n=8．
答：它是八边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.x·x2=x2B.（xy）2=xy2C.（x2）3=x5D.x2+x2=2x2
-
科目： 来源： 题型：
查看答案和解析>>【题目】乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量；无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测），无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．
（1）求主桥AB的长度；
（2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．
（长度均精确到1m，参考数据：
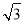≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在等边△ABC中；
（1）如图1，P，Q是BC边上两点，AP＝AQ，∠BAP＝20°，求∠AQB的度数；
（2）点P，Q是BC边上的两个动点(不与点B，C重合)，点P在点Q的左侧，且AP＝AQ，点Q关于直线AC的对称点为M，连接AM，PM.
①依题意将图2补全；②小明通过观察、实验，提出猜想：在点P，Q运动的过程中，始终有PA＝PM，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证PA＝PM，只需证△APM是等边三角形．
想法2：在BA上取一点N，使得BN＝BP，要证PA＝PM，只需证△ANP≌△PCM.……
请你参考上面的想法，帮助小明证明PA＝PM(一种方法即可)． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：
①f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；
②g（m，n）=（﹣m，﹣n），如g（2，1）=（﹣2，﹣1）．
按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（3，2）]等于（ ）
A. （3，2） B. （3．﹣2） C. （﹣3，2） D. （﹣3，﹣2）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，若AB=4，BC=2，且AC的长为偶数，则AC=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市前年PM2.5的年均浓度为50微克/立方米，去年比前年下降了10%，如果今年PM2.5的年均浓度比去年也下降10%，那么今年PM2.5的年均浓度将是微克/立方米．
相关试题
