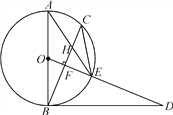
【题目】如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.

求证：（1）BD是⊙O的切线；

（2）若EH=2,AH=6,求CE的长.

参考答案：

【答案】（1）证明见解析（2）4

【解析】试题分析：（1）利用圆周角定理和等角的余角相等即可求出垂直；（2）根据圆周角定理得出两个角相等，近而求相似的三角形，根据已知线段的长度求出所求线段即可.

试题解析：

（1）∵∠ODB＝∠AEC，∠AEC＝∠ABC，

∴∠ODB＝∠ABC，

∵OF⊥BC，

∴∠BFD＝90°，

∴∠ODB＋∠DBF＝90°，

∴∠ABC＋∠DBF＝90°，

即∠OBD＝90°，

∴BD⊥OB，

∴BD是⊙O的切线　

（2）连接AC，

∵OF⊥BC，

∴，

∴∠ECB＝∠CAE，

又∵∠HEC＝∠CEA，

∴△CEH∽△AEC，

∴ ，

∴CE2＝EH·EA

∴CE=4

关闭