搜索
【题目】在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（ ）
A.（2，﹣3）
B.（2，3）
C.（3，﹣2）
D.（﹣2，﹣3）
参考答案：
【答案】A
【解析】 解：根据中心对称的性质，得点P（﹣2，3）关于原点对称点P′的坐标是（2，﹣3）．
故选：A．
【考点精析】掌握关于原点对称的点的坐标是解答本题的根本，需要知道两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）．
-
科目： 来源： 题型：
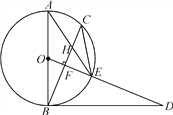
查看答案和解析>>【题目】如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.
求证：（1）BD是⊙O的切线；
（2）若EH=2,AH=6,求CE的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球，其中红球3个（记为A1，A2，A3），黑球2个（记为B1，B2）．
（1）若先从袋中取出m（m＞0）个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A，填空：①若A为必然事件，则m的值为 ②若A为随机事件，则m的取值为
（2）若从袋中随机摸出2个球，正好红球、黑球各1个，用树状图或列表法求这个事件的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知三角形两边的长分别为5、2，第三边长为奇数，则第三边的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线y=
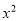+bx+c经过A，B两点，抛物线的顶点为D．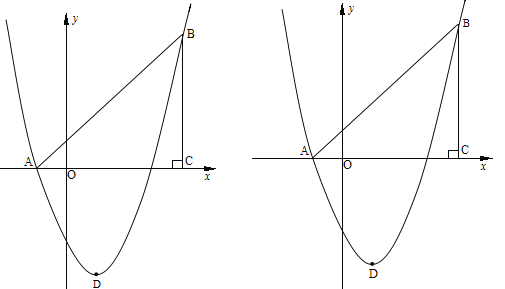
(1)、求b,c的值；
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外)，过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
(3)、在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形? 若存在，求出所有点P的坐标；若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某服装店以每件82元的价格购进了30套保暖内衣，销售时，针对不同的顾客，这30套保暖内衣的售价不完全相同，若以100元为标准，将超过的钱数记为正，不足的钱数记为负，则记录结果如表所示：
售出件数
7
6
7
8
2
售价（元）
+5
+1
0
﹣2
﹣5
请你求出该服装店在售完这30套保暖内衣后，共赚了多少钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】试说明：对于任意自然数n，2n＋4－2n一定能被5整除．
相关试题
