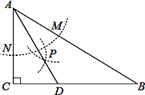
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④![]()
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】试题解析:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,
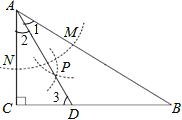
∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
∵∠2=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∴BD=2CD.
故④正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
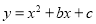 与直线
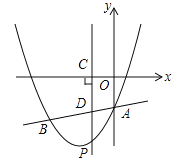
与直线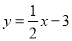 交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】拒绝“餐桌浪费”,刻不容缓.每人一日三餐少浪费一粒米,全国一年就可节省3150万斤,可供9万人吃一年.数据“3150万”用科学记数法表示为( )
A. 0.315×108 B. 3.15×107 C. 31.5×106 D. 315×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;

(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;

(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
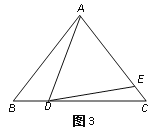
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A到⊙O的最小距离为1,最大距离为3,则⊙O的半径长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线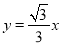 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线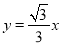 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.(1)如图①所示,若抛物线顶点的纵坐标为
 ,求抛物线的解析式;
,求抛物线的解析式;(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线
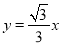 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.平行四边形的对角线相等
B.一组对边平行,一组对边相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.有两对邻角互补的四边形是平行四边形
相关试题

