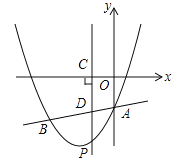
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
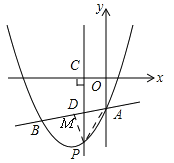
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
参考答案:
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() ),(﹣1,
),(﹣1,![]() ),(﹣3,
),(﹣3,![]() );(3)P(
);(3)P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先确定出点A坐标,然后用待定系数法求抛物线解析式;
(2)先用m表示出PD,当PD=OA=3,故存在以O,A,P,D为顶点的平行四边形,得到![]() ,分两种情况进行讨论计算即可;
,分两种情况进行讨论计算即可;
(3)由△PAM为等腰直角三角形,得到∠BAP=45°,从而求出直线AP的解析式,最后求出直线AP和抛物线的交点坐标即可.
试题解析:(1)∵直线![]() 交于A、B两点,其中点A在y轴上,∴A(0,﹣3),∵B(﹣4,﹣5),∴
交于A、B两点,其中点A在y轴上,∴A(0,﹣3),∵B(﹣4,﹣5),∴![]() ,∴
,∴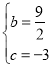 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)存在,设P(m,![]() ),(m<0),∴D(m,
),(m<0),∴D(m,![]() ),∴PD=
),∴PD=![]() .
.
∵PD∥AO,∴当PD=OA=3,故存在以O,A,P,D为顶点的平行四边形,∴![]() ;
;
①当![]() 时,∴
时,∴![]() =
=![]() ,
,![]() =
=![]() (舍),∴
(舍),∴![]() =
=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
②当![]() 时,∴
时,∴![]() =﹣1,
=﹣1,![]() =﹣3.
=﹣3.
Ⅰ、m1=﹣1,∴![]() =
=![]() ,∴P(﹣1,
,∴P(﹣1,![]() );
);
Ⅱ、m2=﹣3,∴![]() =
=![]() ,∴P(﹣3,
,∴P(﹣3,![]() );
);
∴点P的坐标为(![]() ,
,![]() ),(﹣1,
),(﹣1,![]() ),(﹣3,
),(﹣3,![]() );
);
(3)如图,∵△PAM为等腰直角三角形,∴∠BAP=45°,∵直线AP可以看做是直线AB绕点A逆时针旋转45°所得,设直线AP解析式为y=kx﹣3,∵直线AB解析式为![]() ,∴k=
,∴k=![]() =3,∴直线AP解析式为y=3x﹣3,联立:
=3,∴直线AP解析式为y=3x﹣3,联立: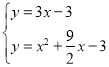 ,∴
,∴![]() =0(舍),
=0(舍),![]() =
=![]() ;
;
当x=![]() 时,y=
时,y=![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家,大家应加倍珍惜水资源,节约用水,据测试,拧不紧的水龙头每秒钟会滴下 2 滴水,每滴水约 0.05 毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开 4 小时后水龙头滴了约______毫升水(用科学记数法表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是确定事件的是( )
A.三角形任意两边之和小于第三边
B.365人中一定至少有两人的生日相同
C.龙口市下周一定会下雨
D.打开电视机,正在播放广告
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果2x2y3与x2yn+1是同类项,那么n的值是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】拒绝“餐桌浪费”,刻不容缓.每人一日三餐少浪费一粒米,全国一年就可节省3150万斤,可供9万人吃一年.数据“3150万”用科学记数法表示为( )
A. 0.315×108 B. 3.15×107 C. 31.5×106 D. 315×105
-
科目: 来源: 题型:
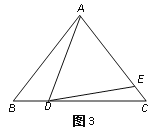
查看答案和解析>>【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;

(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;

(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④
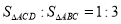
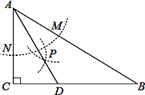
A. 1 B. 2 C. 3 D. 4
相关试题

