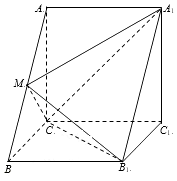
【题目】如图,三棱柱ABC﹣A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=CC1=2,M是AB的中点. 
(1)求证:平面A1CM⊥平面ABB1A1;
(2)求点M到平面A1CB1的距离.
参考答案:
【答案】
(1)解:证明:(Ⅰ)由A1A⊥平面ABC,CM平面ABC,则A1A⊥CM.
由AC=CB,M是AB的中点,则AB⊥CM.
又A1A∩AB=A,则CM⊥平面ABB1A1,
又CM平面A1CM,
所以平面A1CM⊥平面ABB1A1.
(2)解:(Ⅱ)设点M到平面A1CB1的距离为h,
由题意可知 ![]() ,
, ![]() ,
, ![]() .
.
由(Ⅰ)可知CM⊥平面ABB1A1,得:
![]() ,
,
所以,点M到平面A1CB1的距离 ![]() .
.
【解析】(Ⅰ)推导出A1A⊥CM,AB⊥CM.由此能证明平面A1CM⊥平面ABB1A1 . (Ⅱ)设点M到平面A1CB1的距离为h,由 ![]() ,能求出点M到平面A1CB1的距离.
,能求出点M到平面A1CB1的距离.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=sinxcosx+
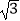 cos2x﹣
cos2x﹣ 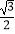 ,将f(x)的图象向右平移
,将f(x)的图象向右平移  个单位,再向上平移1个单位,得到y=g(x)的图象.若对任意实数x,都有g(a﹣x)=g(a+x)成立,则
个单位,再向上平移1个单位,得到y=g(x)的图象.若对任意实数x,都有g(a﹣x)=g(a+x)成立,则 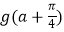 =( )
=( )
A.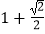
B.1
C.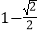
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】设正实数x,y,z满足x2﹣3xy+4y2﹣z=0.则当
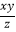 取得最大值时,
取得最大值时, 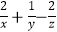 的最大值为( )
的最大值为( )
A.0
B.1
C.
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某高新技术公司要生产一批新研发的A款手机和B款手机,生产一台A款手机需要甲材料3kg,乙材料1kg,并且需要花费1天时间,生产一台B款手机需要甲材料1kg,乙材料3kg,也需要1天时间,已知生产一台A款手机利润是1000元,生产一台B款手机的利润是2000元,公司目前有甲、乙材料各,则在300kg不超过120天的情况下,公司生产两款手机的最大利润是元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下2×2列联表:
男生
女生
合计
挑同桌
30
40
70
不挑同桌
20
10
30
总计
50
50
100
(Ⅰ)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
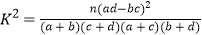 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线E:y2=4x的准线为l,焦点为F,O为坐标原点.
(1)求过点O,F,且与l相切的圆的方程;
(2)过F的直线交抛物线E于A,B两点,A关于x轴的对称点为A′,求证:直线A′B过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x3﹣
x3﹣  x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
x2+logax,(a>0且a≠1)为定义域上的增函数,f'(x)是函数f(x)的导数,且f'(x)的最小值小于等于0. (Ⅰ)求a的值;
(Ⅱ)设函数 ,且g(x1)+g(x2)=0,求证:
,且g(x1)+g(x2)=0,求证: 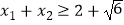 .
.
相关试题

