搜索
【题目】设正实数x，y，z满足x2﹣3xy+4y2﹣z=0．则当 
取得最大值时， 
的最大值为（ ）
A.0
B.1
C.
D.3
参考答案：
【答案】B
【解析】解：∵x2﹣3xy+4y2﹣z=0， ∴z=x2﹣3xy+4y2 ， 又x，y，z均为正实数，
∴ 
= 
= 
≤ 
=1（当且仅当x=2y时取“=”），
∴ 
=1，此时，x=2y．
∴z=x2﹣3xy+4y2=（2y）2﹣3×2y×y+4y2=2y2 ，
∴ 
+ 
﹣ 
= + ﹣ 
=﹣ 
+1≤1，当且仅当y=1时取得“=”，满足题意．
∴ 
的最大值为1．
故选B．
依题意，当 取得最大值时x=2y，代入所求关系式f（y）= + ﹣ ，利用配方法即可求得其最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．
（1）试问去年每吨大蒜的平均价格是多少元？
（2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列四个命题： ①回归直线
恒过样本中心点 
；
②“x=6”是“x2﹣5x﹣6=0”的必要不充分条件；
③“x0∈R，使得x02+2x0+3＜0”的否定是“对x∈R，均有x2+2x+3＞0”；
④“命题p∨q”为真命题，则“命题p∧q”也是真命题．
其中真命题的个数是（ ）
A.0
B.1
C.2
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知f（x）=sinxcosx+
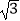cos2x﹣ 
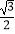，将f（x）的图象向右平移 
个单位，再向上平移1个单位，得到y=g（x）的图象．若对任意实数x，都有g（a﹣x）=g（a+x）成立，则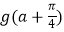 
=（ ）
A.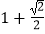
B.1
C.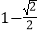
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】某高新技术公司要生产一批新研发的A款手机和B款手机，生产一台A款手机需要甲材料3kg，乙材料1kg，并且需要花费1天时间，生产一台B款手机需要甲材料1kg，乙材料3kg，也需要1天时间，已知生产一台A款手机利润是1000元，生产一台B款手机的利润是2000元，公司目前有甲、乙材料各，则在300kg不超过120天的情况下，公司生产两款手机的最大利润是元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，三棱柱ABC﹣A1B1C1中，A1A⊥平面ABC，∠ACB=90°，AC=CB=CC1=2，M是AB的中点．
（1）求证：平面A1CM⊥平面ABB1A1；
（2）求点M到平面A1CB1的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌，得到如下2×2列联表：
男生
女生
合计
挑同桌
30
40
70
不挑同桌
20
10
30
总计
50
50
100
（Ⅰ）从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本，现从这5人中随机选取3人做深度采访，求这3名学生中至少有2名要挑同桌的概率；
（Ⅱ）根据以上2×2列联表，是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关？
下面的临界值表供参考：P（K2≥k0）
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：
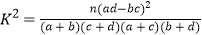，其中n=a+b+c+d）
相关试题
