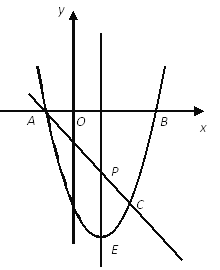
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
参考答案:
【答案】(1)抛物线的解析式y=x2-2x-3,直线AC的函数解析式是y=-x-1;(2)PE的最大值=![]() ;
;
(3)F点的坐标是(-3,0),(1,0),(4-![]() ,0),(4+
,0),(4+![]() ,0).
,0).
【解析】
试题(1)A(-1,0),B(3,0),C(2,-3),该二次函数与x轴交点计算得到
即:![]() ,故A(-1,0)C(2,-3)
,故A(-1,0)C(2,-3)
故:直线AC解析式:y=-x-1 3分
(2)设P(x,-x-1),E(x,x2-2x-3),(![]() )
)
PE=-x2+x+2=-(x-![]() )2+
)2+![]()
![]() ,最大值为
,最大值为![]() 5分
5分
(3)四个点F1(1,0);F2(4+![]() ,0); F3(4-
,0); F3(4-![]() ,0);F4(-3,0) 4分
,0);F4(-3,0) 4分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段的长分别为
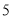 厘米,
厘米, 厘米,
厘米,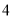 厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形.
厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2 - 2(1-m)x+m2的两实数根为x1,x2.
(1)求m的取值范围;
(2)设
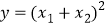 ,当m为何值时,y有最小值,求y的最小值.
,当m为何值时,y有最小值,求y的最小值. -
科目: 来源: 题型:
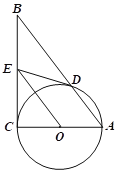
查看答案和解析>>【题目】如图在RtΔABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,求△ADO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
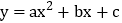 (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是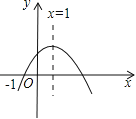
A. a>0 B. 当﹣1<x<3时,y>0
C. c<0 D. 当x≥1时,y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数
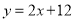 的图像分别交
的图像分别交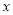 轴、
轴、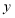 轴于
轴于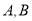 两点.过点
两点.过点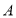 的直线交
的直线交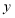 轴正半轴于点
轴正半轴于点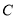 ,且点
,且点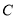 为线段
为线段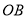 的中点.
的中点.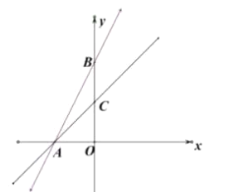
(1)求直线
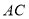 的表达式;
的表达式;(2)如果四边形
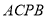 是平行四边形,求点
是平行四边形,求点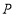 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
A. ①② B. ②③ C. ①②④ D. ①②③④
相关试题

