搜索
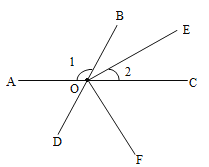
【题目】如图所示，点
、
、
在同一直线上，
是
的平分线，
，
，
.
（1）求
的度数（请写出解题过程）.
（2）如以
为一边，在
的外部画
，问边
与边
成一直线吗？请说明理由.
参考答案：
【答案】（1）
；（2）边
与边
成一直线，理由详见解析.
【解析】
（1）因为OE是∠BOC的平分线所以∠BOC=2∠2，再根据点A、O、C在一直线上，求出∠1和∠2关于x的关系式，列出等式求出x的值；
（2）根据∠EOF=∠EOC+∠COF=90°和∠EOC=
∠BOC，∠FOC=∠DOC，∠BOC+∠DOC=90°，得出∠BOC+∠DOC=180°，进而可可判断边OD与边OB成一直线．
（1）因为
是
的平分线，所以
，
因为点
、
、
在同一直线上，所以
，
又因为
，
，
所以
，
解得：
，
（2）边与边成一直线.
理由：因为
，
又因为
，
.
∴
，
即
，所以点
、、
在同一直线上，即边与边成一直线.
-
科目： 来源： 题型：
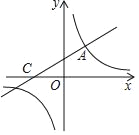
查看答案和解析>>【题目】如图，直线
与双曲线
相交于点A(m，3)，与x轴交于点C.(1)求双曲线的解析式；
(2)点P在x轴上，如果△ACP的面积为3，求点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】2017年5月14日至15日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元？
(2)若甲、乙两种商品的销售总收入不低于5400万元，则至少销售甲种商品多少万件？
-
科目： 来源： 题型：
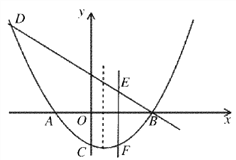
查看答案和解析>>【题目】如图，已知拋物线
（k为常数，且k＞0）与x轴的交点为A、B，与y轴的交点为C，经过点B的直线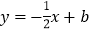
与抛物线的另一个交点为D.(1)若点D的横坐标为x= -4，求这个一次函数与抛物线的解析式；
(2)若直线m平行于该抛物线的对称轴，并且可以在线段AB间左右移动，它与直线BD和抛物线分别交于点E、F，求当m移动到什么位置时，EF的值最大，最大值是多少？
(3)问原抛物线在第一象限是否存在点P，使得△APB∽△ABC？若存在，请求出这时k的值；若不存在，请说明理由.
-
科目： 来源： 题型：
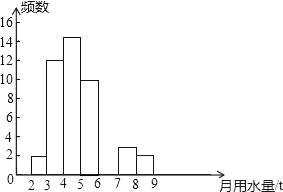
查看答案和解析>>【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．
月均用水量（单位：t）
频数
百分比
2≤x＜3
2
4%
3≤x＜4
12
24%
4≤x＜5
5≤x＜6
10
20%
6≤x＜7
12%
7≤x＜8
3
6%
8≤x＜9
2
4%
（1）请根据题中已有的信息补全频数分布表和频数分布直方图；
（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你估计总体小王所居住的小区中等用水量家庭大约有多少户？
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列举法（画树状图或列表）求抽取出的2个家庭来自不同范围的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】实验探究：
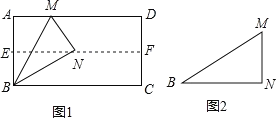
(1)如图1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开；再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN.请你观察图1，猜想∠MBN的度数是多少，并证明你的结论.
(2)将图1中的三角形纸片BMN剪下，如图2，折叠该纸片，探究MN与BM的数量关系，写出折叠方案，并结合方案证明你的结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．其中x表示时间，y表示张强离家的距离．根据图象回答下列问题：
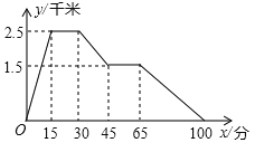
(1)体育场离张强家_____千米；
(2)体育场离文具店_____千米，张强在文具店停留了_____分；
(3)张强从文具店回家的平均速度是________千米/分
相关试题
