【题目】唐山世园会期间,游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收31万元.而该游乐场开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx.若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数.
(1)若维修保养费用第1个月为2万元,第2个月为4万元,求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大?并求出最大收益.
参考答案:
【答案】(1)y=x2+x;(2)g=﹣x2+30 x﹣150;(3)设施开放15个月后,游乐场的纯收益达到最大,最大收益为75万元.
【解析】
(1)根据题意确定x,y的两组对应值求y的函数关系式;
(2)根据纯收益g=开放后每月可创收31万元×月数x﹣游乐场投资150万元﹣从第1个月到第x个月的维修保养费用累计y,列出函数关系式;
(3)求函数最大值,及g>0时,x的值,可确定回收投资的月份.
解:(1)由题意得:x=1时y=2;
x=2时,y=2+4=6代入得:
![]()
解之得:![]()
∴y=x2+x;
(2)由题意得:
g=31x﹣150﹣(x2+x)
=﹣x2+30 x﹣150;
(3)g=﹣x2+30x﹣150=﹣(x﹣15)2+75,
∴当x=15时,g最大值=75,
即设施开放15个月后,游乐场的纯收益达到最大,最大收益为75万元.
-
科目: 来源: 题型:
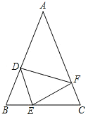
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)直接写出当∠A为多少度时,△DEF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)数轴上有A、B两点,若A点对应的数是﹣2,且A、B两点间的距离为3,则点B对应的数是________;
(2)已知线段AB=12cm,直线AB上有一点C,且BC=4cm,M是AC的中点,AM的长为________;
(3)已知∠AOB=3∠BOC,∠BOC=30°,则∠AOC=________;
(4)已知等腰三角形两边长为17、8,求三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有
 本,最多的有
本,最多的有 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:本数(本)
频数(人数)
频率












合计



(
 )统计图表中的
)统计图表中的 __________,
__________, __________,
__________, __________.
__________.(
 )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.(
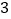 )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.(
 )若该校八年级共有
)若该校八年级共有 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读 本及以上的人数.
本及以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
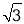 ).
).(1)求∠BAO的度数;
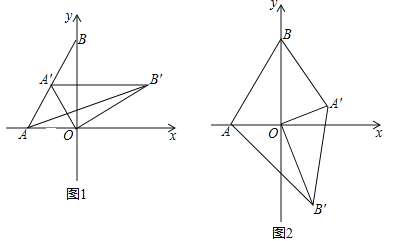
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
-
科目: 来源: 题型:
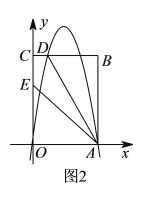
查看答案和解析>>【题目】如图
 ,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线
,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线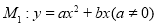 过A,D两点.
过A,D两点.(
 )求点D的坐标和抛物线M1的表达式.
)求点D的坐标和抛物线M1的表达式.(
 )点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.
)点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.(
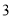 )如图
)如图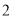 ,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.
,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.①设点D平移后的对应点为点D',当点D'恰好落在直线AE上时,求m的值.
②当
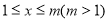 时,若抛物线M2与直线AE有两个交点,求m的取值范围.
时,若抛物线M2与直线AE有两个交点,求m的取值范围.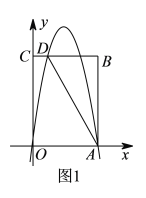
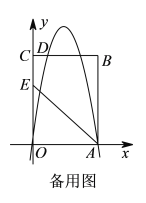
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2
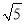 ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.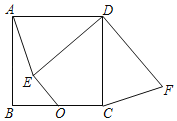
相关试题

