【题目】设函数![]() (其中k为常数).
(其中k为常数).
(1)当k=-2时,函数y存在最值吗?若存在,请求出这个最值;
(2)在x>0时,要使函数y的的值随x的增大而减小,求k应满足的条件;
(3)若函数y的图象与x轴交于A、B两点,与y轴交于点C,求能使△ABC为等腰三角形的k的值.(分母保留根号,不必化简)
参考答案:
【答案】(1)x=-![]() 时,y最大=
时,y最大=![]() ;(2)k≤0;(3)k=3,k=
;(2)k≤0;(3)k=3,k=![]() ,k=
,k=![]() ,k=-
,k=-![]() .
.
【解析】
试题分析:本题考查二次函数的有关知识、一次函数的有关知识,掌握函数的性质是解决问题的关键,学会分类讨论的思想,属于中考常考题型.
(1)把k=-2代入抛物线解析式得到y=-2x2-5x-3,根据顶点坐标公式即可解决.
(2)分两种情形讨论当k=0时,y=-3x-3为一次函数,k=-3<0,则当x>0时,y随x的增大而减小;当k≠0时,y=(kx-3)(x+1)=kx2+(k-3)x-3为二次函数,由不等式组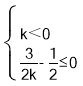 解决.
解决.
(3)分三种情形讨论:当k>0时①AC=BC,②AC=AB,③AB=BC分别列出方程解决;当k<0时,B只能在A的左侧,只有AC=AB列出方程解决,当k=0时,不合题意.
试题解析:(1)当k=-2时,函数y=(-2x-3)(x+1)=-(2x+3)(x+1),
函数为二次函数,且二次项系数小于0,故函数存在最大值,
当x=-![]() 时,y最大=
时,y最大=![]() ;
;
(2)当k=0时,y=-3x-3为一次函数,-3<0,则当x>0时,y随x的增大而减小;
当k≠0时,y=(kx-3)(x+1)为二次函数,其对称轴为直线x=![]() =
=![]() -
-![]() ,要使当x>0时,y随x的增大而减小,则抛物线的开口必定朝下,且对称轴不在y轴的右边.
,要使当x>0时,y随x的增大而减小,则抛物线的开口必定朝下,且对称轴不在y轴的右边.
故得,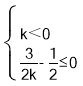 ,
,
解得k<0,
综上所述,k应满足的条件是:k≤0.
(3)由题意得,k≠0,函数为二次函数.
由所给的抛物线解析式可得A,C为定值A(-1,0),C(0,-3)则AC=![]() ,而B(
,而B(![]() ,0),
,0),
(1)k>0,则可得,
①AC=BC,则有![]() =
=![]() ,可得k=3,
,可得k=3,
②AC=AB,则有![]() +1=
+1=![]() ,可得k=
,可得k=![]() ,
,
③AB=BC,则有![]() +1=
+1=![]() ,可得k=
,可得k=![]() ,
,
④k<0,B只能在A的左侧,
只有AC=AB,则有-![]() -1=
-1=![]() ,可得k=-
,可得k=-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 绝对值等于本身的数是1、-1、0
B. 一个负数的绝对值是它的相反数
C. 如果两个数的绝对值相等,那么这两个数相等
D. 平方等于9的数是3
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:71=7,72=49,73=343,74=2401,75=16807,…那么72007+1的个位数字是( )
A. 8 B. 4 C. 2 D. 0
-
科目: 来源: 题型:
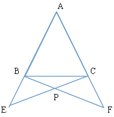
查看答案和解析>>【题目】在△ABC中,AB=AC,点E,F分别在AB,AC的延长线上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是杭州市2016年2月份的空气质量指数的AQI折线统计图,空气质量指数AQI的值在不同的区间,就代表了不同的空气质量水平(如在0–50之间,代表“优”;51–100之间,代表“良”;101–150之间,代表“轻度污染”等。)以下是关于杭州市2016年2月份空气质量天数情况统计图.
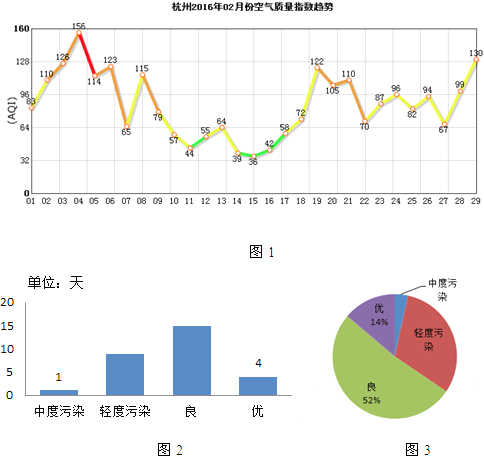
(1)根据三个图表中的信息,请补全条形统计图和扇形统计图中缺失的数据;(扇形统计图中的数据精确到1%)
(2)求出图3中表示轻度污染的扇形圆心角的度数;(结果精确到度)
(3)在杭州,有一种“蓝”叫“西湖蓝”。现在的一年中,我们至少有超过一半以上的时间能看见“西湖蓝”.请估算2016年一年杭州的空气质量为优良的天数.(一年按365计,精确到天)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,AB//CD,AE平分MAB交CD于点F,NF⊥CD,垂足为点F,
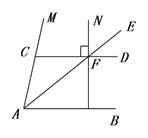
(1)求证:CAF=EFD
(2)若MCD=80,求NFE的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,∠BAC=120°,点D为AB中点,点E在BC边上,CE=3BE,AE与CD交于点F, 若AF=
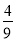 ,则FC的长为________________.
,则FC的长为________________.
相关试题

