【题目】为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

参考答案:
【答案】(1)当0≤x≤12时, ![]() ;当x≥12时,
;当x≥12时, ![]() ;(2)4小时.
;(2)4小时.
【解析】试题分析:首先根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,将数据代入用待定系数法可得反比例函数的关系式;进一步求解可得答案.
试题解析:(1)当0≤x≤12时, ![]() ;当x≥12时,
;当x≥12时, ![]() 。
。
(2)当y=0.45时,代入![]() 中,得x=240(分钟)=4(小时),
中,得x=240(分钟)=4(小时),
则从药物释放开始,至少需要经过4小时后,学生才能进入教室.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如下表:
甲
8
9
7
9
8
6
7
8
10
8
乙
6
7
9
7
9
10
8
7
7
10
且
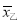 =8,
=8,  =1.8.根据上述信息完成下列问题:
=1.8.根据上述信息完成下列问题:(1)将甲运动员的折线统计图补充完整.
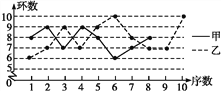
(2)求乙运动员射击训练成绩的众数和中位数.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【新知理解】
如图①,若点
 、
、 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点 ,使
,使 的值最小.
的值最小.作法:作点
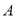 关于直线l的对称点
关于直线l的对称点 ,连接
,连接 交直线l于点
交直线l于点 ,则点
,则点 即为所求.
即为所求.【解决问题】
如图②,
 是边长为6cm的等边三角形
是边长为6cm的等边三角形 的中线,点
的中线,点 、
、 分别在
分别在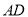 、
、 上,则
上,则 的最小值为 cm;
的最小值为 cm;【拓展研究】
如图③,在四边形
 的对角线
的对角线 上找一点
上找一点 ,使
,使 .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合,连接CE.
(1)△ABC旋转了多少度?
(2)连接CE,试判断△AEC的形状.
(3)若∠ACE=20°,求∠AEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列证明过程填空:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C

证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°
∴BD∥EF ( )
∴∠4=_____ ( )
∵∠1=∠4
∴∠1=_____
∴DG∥BC ( )
∴∠ADG=∠C( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样的题目:把方程
 x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:(1)下面式子中是方程
 x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)①
 x2-x-2=0,②-
x2-x-2=0,②-  x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤
x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤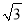 x2-2
x2-2 x-4
x-4 =0.
=0.(2)方程
 x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.

相关试题

