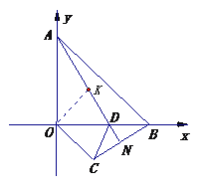
【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交X轴于B点,A(0,6),B(6,0).点D是线段BO上一点,BN⊥AD交AD的延长线于点N.
(1)如图,若OM∥BN交AD于点M.点O作0G⊥BN,交BN的延长线于点G,求证:AM=BG

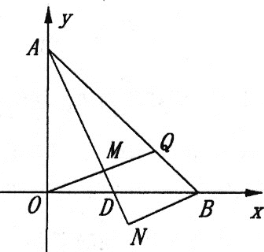
(2)如图,若∠ADO=67.5°,OM∥BN交AD于点M,交AB于点Q,求![]() 的值.
的值.
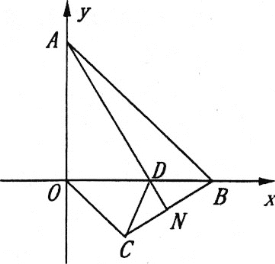
(3)如图,若OC∥AB交BN的延长线于点C.请证明:∠CDN+2∠BDN=180°.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)欲证明AM=BG,只要证明△AOM≌△BOG即可;
(2)在AD上截取AH=OQ,连接OH,先证明△AOH≌△△OBQ,推出∠AOH=∠OBQ=45°,推出HD=2MD.
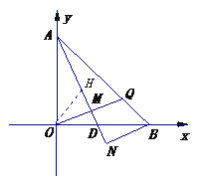
(3)如图,作OE平分∠AOB交AD于K.只要证明△AOK≌△OBC,推出OK=OC,再证明△ODK≌△ODC,推出∠ODK=∠ODC,由∠ODK=∠BDN,可得∠ODC=∠BDN,由此即可解决问题.
(1) 在△AOM和△BOG中
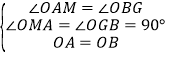
∴△AOM≌△△BOG
∴AM=BG.
② 在AD上截取AH=OQ,连接OH,
∵∠ADO=67.5°∴∠OAD=∠BOQ=22.5°
易证∴△AOH≌△△OBQ
∴∠AOH=∠OBQ=45°
∴∠HOM=90°-45°-22.5°=22.5°=∠BOQ
有三线合一性质得HD=2MD
∴![]() =
=![]() =
=![]() =
=![]()
(3)作∠AOD的角平分线交AD于K
∵0C∥AB ∴∠ABO=∠BOC=∠AOK=∠BOK=450
 在△AOK和△BOC中
在△AOK和△BOC中
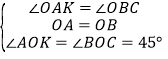
∴△AOK≌△△BOC
∴OK=OC
在△KOD和△DOC中
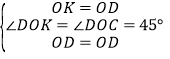
∴△KOD≌△△DOC
∴∠ODC=∠ODK=∠BDN
∴∠CDN+2∠BDN=180°.
-
科目: 来源: 题型:
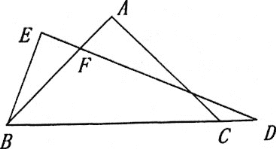
查看答案和解析>>【题目】已知△ABC中,AB=AC,∠BAC=90°.
(1)如图,若CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论
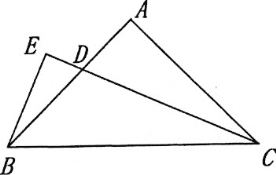
(2)如图,若点D在线段BC延长上,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE和FD的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的四个三角形中,不能由如图的三角形经过旋转或平移得到的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
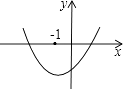
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴x=﹣1,下列五个代数式ab、ac、a﹣b+c、b2﹣4ac、2a+b中,值大于0的个数为( )
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣6x﹣16=0
(2)(x﹣3)2=3x(x﹣3)
(3)(x+3)(x﹣2)=50
(4)(2x+1)2+3(2x+1)+2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:
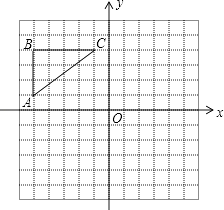
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC关于原点O对称的△A2B2C2;
(2)点C1的坐标是;点C2的坐标是;
(3)试判断:△A1B1C1与△A2B2C2是否关于x轴对称?(只需写出判断结果) . -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
相关试题

