【题目】如图,点![]() 为原点,
为原点,![]() 、
、![]() 为数轴上两点,
为数轴上两点,![]() ,且
,且![]()
![]()
(1)![]() 、
、![]() 对应的数分别为________、________;
对应的数分别为________、________;
(2)点![]() 、
、![]() 分别以
分别以![]() 个单位/秒和
个单位/秒和![]() 个单位/秒的速度相向而行,则几秒后
个单位/秒的速度相向而行,则几秒后![]() 、
、![]() 相距
相距![]() 个单位长度?
个单位长度?
(3)动点![]() 从点
从点![]() 出发,沿数轴正方向运动,
出发,沿数轴正方向运动,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点.在点
的中点.在点![]() 运动的过程中,线段
运动的过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段![]() 的长.
的长.
参考答案:
【答案】(1)-10;5;(2)2秒或![]() 秒;(3)线段MN的长度不变化,都等于7.5,理由见详解
秒;(3)线段MN的长度不变化,都等于7.5,理由见详解
【解析】
(1)根据题意可得出![]() ,继而可得出A,B对应的数;
,继而可得出A,B对应的数;
(2)分相遇前与相遇后两种情况,设时间为x,列一元一次方程求解即可;
(3)线段MN的长度不变化,分类讨论:①点P在点A,B两点之间运动时,②点P运动到点B的右侧时,利用中点的定义和线段的和差易求出MN.
解:(1)∵AB=15,OA:OB=![]()
∴![]() ,
,
即点A对应的数为-10,点B对应的数为5;
(2)设x秒后,A,B两点相距1个单位长度,由题意得出:
当A,B相遇前,4x+3x=15-1
7x=14,
解得,x=2;
当A,B相遇后,4x+3x=15+1
7x=16
解得,![]() .
.
答:2秒或![]() 秒后A,B两点相距1个单位长度.
秒后A,B两点相距1个单位长度.
(3)线段MN的长度不变化,都等于7.5, 理由如下:
分两种情况:
点P在点A,B两点之间运动时:

![]() ;
;
点P运动到点B的右侧时:

![]() ;
;
∴综上所述,线段MN的长度不变化,其值都等于7.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线y=
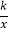 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )
,则k的值是( )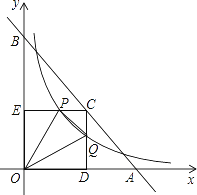
A. 4 B. 2 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过
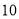 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过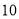 吨时,超出
吨时,超出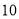 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家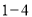 月份用水量和交费情况:
月份用水量和交费情况:月份
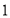
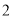
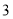
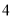
用水量(吨)
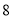
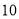
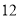
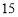
费用(元)
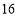
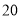
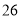
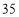
请根据表格中提供的信息,回答以下问题:
(1)若小明家
 月份用水量为
月份用水量为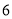 吨,则应缴水费________元;
吨,则应缴水费________元;(2)若某户某月用了
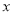 吨水(
吨水(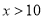 ),应付水费________元;
),应付水费________元;(3)若小明家
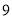 月份交纳水费
月份交纳水费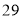 元,则小明家
元,则小明家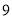 月份用水多少吨?
月份用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】对点(x,y)的一次操作变换记为p1(x,y),定义其变换法则如下:p1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).例如:p1(1,2)=(3,-1),p2(1,2)=p1(p1(1,2))=p1(3,-1)=(2,4),p3(1,2)=p1(p2(1,2))=p1(2,4)=(6,-2).则p2014(1,-1)=( )
A.(0,21006) B.(21007,-21007) C.(0,-21006) D.(21006,-21006)
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
-
科目: 来源: 题型:
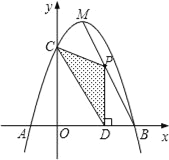
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
相关试题

