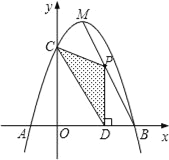
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)解析式为y=﹣x2+2x+3;(2)当m=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ; (3)存在,P点坐标为(
; (3)存在,P点坐标为(![]() ,3)或(﹣3+3
,3)或(﹣3+3![]() ,12﹣6
,12﹣6![]() )时,△PCD为直角三角形.
)时,△PCD为直角三角形.
【解析】试题分析:(1)把B点和C点坐标代入y=﹣x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)把(1)中的一般式配成顶点式可得到M(1,4),设直线BM的解析式为y=kx+n,再利用待定系数法求出直线BM的解析式,则P(m,﹣2m+6)(1≤m<3),于是根据三角形面积公式得到S=﹣m2+3m,然后根据二次函数的性质解决问题;
(3)讨论:∠PDC不可能为90°;当∠DPC=90°时,易得﹣2m+6=3,解方程求出m即可得到此时P点坐标;当∠PCD=90°时,利用勾股定理得到和两点间的距离公式得到m2+(﹣2m+3)2+32+m2=(﹣2m+6)2,
然后解方程求出满足条件的m的值即可得到此时P点坐标.
试题解析:(1)把B(3,0),C(0,3)代入y=﹣x2+bx+c得![]() ,解得
,解得![]() ,
,
所以抛物线解析式为y=﹣x2+2x+3;
(2)S有最大值.理由如下:
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴M(1,4),
设直线BM的解析式为y=kx+n,
把B(3,0),M(1,4)代入得![]() ,解得
,解得![]() ,
,
∴直线BM的解析式为y=﹣2x+6,
∵OD=m,
∴P(m,﹣2m+6)(1≤m<3),
∴S=![]() m(﹣2m+6)=﹣m2+3m=﹣(m﹣
m(﹣2m+6)=﹣m2+3m=﹣(m﹣![]() )2+
)2+![]() ,
,
∵1≤m<3,
∴当m=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(3)存在.
∠PDC不可能为90°;
当∠DPC=90°时,则PD=OC=3,即﹣2m+6=3,解得m=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,3),
,3),
当∠PCD=90°时,则PC2+CD2=PD2,即m2+(﹣2m+3)2+32+m2=(﹣2m+6)2,
整理得m2+6m﹣9=0,解得m1=﹣3﹣3![]() (舍去),m2=﹣3+3
(舍去),m2=﹣3+3![]() ,
,
当m=﹣3+3![]() 时,y=﹣2m+6=6﹣6
时,y=﹣2m+6=6﹣6![]() +6=12﹣6
+6=12﹣6![]() ,此时P点坐标为(﹣3+3
,此时P点坐标为(﹣3+3![]() ,12﹣6
,12﹣6![]() ),
),
综上所述,当P点坐标为(![]() ,3)或(﹣3+3
,3)或(﹣3+3![]() ,12﹣6
,12﹣6![]() )时,△PCD为直角三角形.
)时,△PCD为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正比例函数的图像经过点(﹣1,3),则这个正比例函数的表达式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形两对角之和为200度,则此平行四边形的最大内角为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣5的绝对值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=-3x-2向上平移3个单位长度后得到的直线解析式是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
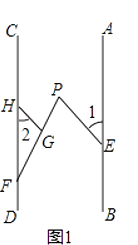
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;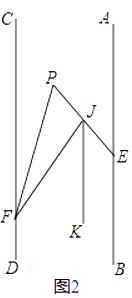
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
相关试题

