【题目】已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )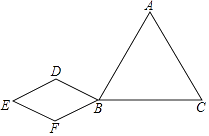
A.甲、乙都对
B.乙对甲不对
C.甲对乙不对
D.甲、乙都不对
参考答案:
【答案】A
【解析】解:连接DF,AF,CD,如图,
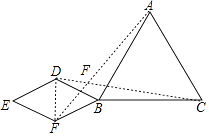
∵四边形BDEF为菱形,
∴BD=BF,
而DF=BD,
∴△BDF为等边三角形,
∴∠DBF=60°,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴∠ABF=∠CBD,
∴△ABF绕点B顺时针旋转60°可得到△CBD,
∴AF=CD,∠FBA=∠DBC,
∴∠AFC=∠ABC=60°,
即直线AF和直线CD所夹的锐角的度数为60°.
所以答案是:A.
【考点精析】根据题目的已知条件,利用等边三角形的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A表示的数为
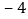 ,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动
,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动 设运动时间为t秒
设运动时间为t秒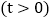 .
.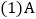 ,B两点间的距离等于______,线段AB的中点表示的数为______;
,B两点间的距离等于______,线段AB的中点表示的数为______;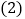 用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;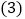 求当t为何值时,
求当t为何值时,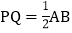 ?
? 若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:已知:A=2a2+3ab﹣2a﹣1,B=﹣a2+ab﹣1.
(1)求2A﹣3B;
(2)若A+2B的值与a的取值无关,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能够铺满地面的组合图形是( )
A. 正八边形和正方形 B. 正方形和正三角形
C. 正六边形和正方形 D. 正六边形和正三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

相关试题

