搜索
【题目】如图，∠AOB=45°，点M，N在边OA上，OM=3，ON=7，点P是直线OB上的点，要使点P，M，N构成等腰三角形的点P有（ ）个．
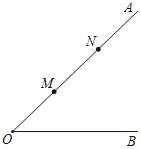
A. 1 B. 2 C. 3 D. 4
参考答案：
【答案】C
【解析】
先求出点M、N到在OB的距离，再根据等腰三角形的判定逐个画出即可．
过M作MM′⊥OB于M′，过N作NN′⊥OB于N′，如图所示：
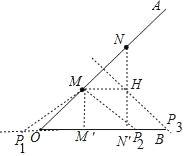
∵OM=3，ON=7，∠AOB=45°，
∴MN=4，MM′=OM×sin45°=
＜4，NN′=ON×sin45°=
＞4，MH=M′N′=4×sin45°=2
＜4，
所以只有一小两种情况：①以M为圆心，以4为半径画弧，交直线OB于P1、P2，此时△NP1M和△NMP2都是等腰三角形；
②作线段MN的垂直平分线，交直线PB于P3，此时△MNP3是等腰三角形，
即有3个点P符合，
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在△ABC中，AB=AC。
（1）若D为AC的中点，BD把三角形的周长分为24cm和30cm两部分，求△ABC三边的长；
（2）若D为AC上一点，试说明AC＞
（BD+DC）。 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A=110°，∠B=85°将△BMN沿着MN翻折，得到△FMN，若MF∥AD，FN∥DC，则∠C的度数为（ ）
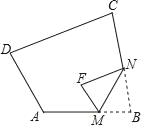
A. 70° B. 80° C. 90° D. 100°
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，△ABC中，∠C=90°，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，求△BCD的周长为；
（2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长等于AD的长．
①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；
②在图3中补全图形，求∠EOF的度数；
③若
， 求
的值
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠ABC＝∠DCB，添加一个条件，使△ABC≌△DCB，你添加的条件是_____．（注：只需写出一个条件即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料后解决问题：
计算：（2+1）（22+1）（24+1）（28+1）．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：
（2+1）（22+1）（24+1）（28+1）
=（2﹣1）（2+1）（22+1）（24+1）（28+1）
=（22﹣1）（22+1）（24+1）（28+1）
=（24﹣1）（24+1）（28+1）
=（28﹣1）（28+1）
=216﹣1
请你根据以上解决问题的方法，试着解决：
（3+1）（32+1）（34+1）（38+1）…（364+1）=__
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知点A（3，0），B（0，4），将△BOA绕点A按顺时针方向旋转得△CDA，连接OD．当∠DOA=∠OBA时，直线CD的解析式为________
相关试题
