【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为 . 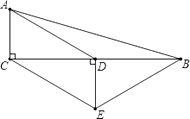
参考答案:
【答案】10+2 ![]()
【解析】解:∵∠ACB=90°,DE⊥BC, ∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,
∴BC=2CD=4 ![]() ,
,
在△ABC中,∠ACB=90°,
由勾股定理得AB= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2 ![]() ,
,
所以答案是:10+2 ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和三角形中位线定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接任意四边形的各边中点得到的四边形一定是( )
A.正方形
B.矩形
C.菱形
D.平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题为假命题的是( )
A. 三角形三个内角的和等于180° B. 三角形两边之和大于第三边
C. 三角形的外角大于任何一个和它不相邻的内角 D. 若a>0,b<0,则a+b>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )

A.15°
B.20°
C.25°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
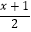 >
> 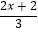 ﹣1,并写出它的正整数解.
﹣1,并写出它的正整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解被拆迁236户家庭对拆迁补偿方案是否满意,小明利用周末调查了其中的50户家庭,有32户对方案表示满意,在这一调查中,样本容量为________.
-
科目: 来源: 题型:
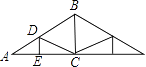
查看答案和解析>>【题目】如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=m.
相关试题

