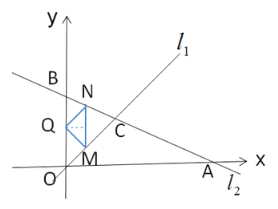
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.

(1)求点![]() ,点
,点![]() ,点
,点![]() 的坐标,并求出
的坐标,并求出![]() 的面积;
的面积;
(2)若直线 ![]() 上存在点
上存在点![]() (不与
(不与![]() 重合),满足
重合),满足![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)在![]() 轴右侧有一动直线平行于
轴右侧有一动直线平行于![]() 轴,分别与
轴,分别与![]() ,
,![]() 交于点
交于点![]() ,且点
,且点![]() 在点
在点![]() 的下方,
的下方,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出满足条件的点
为等腰直角三角形?若存在,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把![]() 和
和![]() 分别代入
分别代入![]() 可求出点
可求出点![]() ,点
,点![]() 坐标,联立直线
坐标,联立直线![]() 和直线
和直线![]() 解析式可求得点
解析式可求得点![]() 的坐标,然后根据B,C坐标可求
的坐标,然后根据B,C坐标可求![]() 的面积;
的面积;
(2)作![]() 轴于点
轴于点![]() ,
,![]() 轴于点E,根据
轴于点E,根据![]() 可得
可得![]() ,代入
,代入![]() 的解析式
的解析式![]() 可求出点
可求出点![]() 的坐标;
的坐标;
(3)分情况讨论:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别求出点
时,分别求出点![]() 的坐标即可.
的坐标即可.
解:(1)把![]() 代入
代入![]() 可得
可得![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 可得
可得![]() ,
,
∴![]() ,
,
联立直线![]() 和直线
和直线![]() 得:
得: ,解得:
,解得:![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
∵ ![]() ,
, ![]() ,
,
∴![]() ;
;
(2)作![]() 轴于点
轴于点![]() ,
,![]() 轴于点E,
轴于点E,
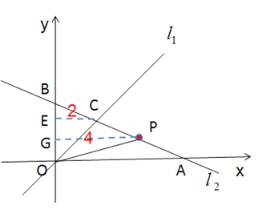
∵![]()
∴![]()
∴![]() ,
,
∴把![]() 代入
代入![]() 的解析式
的解析式![]() ,得
,得![]() ,
,
∴![]() 存在点
存在点![]() 满足
满足![]() ;
;
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ,
,
设动直线为![]() ,由题可得
,由题可得![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
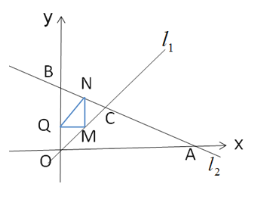
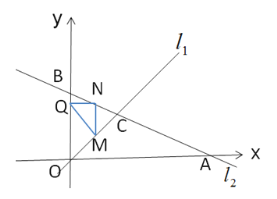
∴![]() (如图).
(如图).
①当![]() 时,有
时,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() 轴,
轴,
∴点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 时,有
时,有![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() 轴,
轴,
∴点![]() 的坐标为
的坐标为![]() ;
;
③当![]() 时,点
时,点![]() 到
到![]() 的距离
的距离![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴点![]() 的坐标为
的坐标为![]() .
.
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.
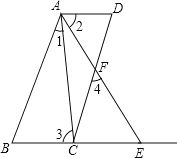
解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
-
科目: 来源: 题型:
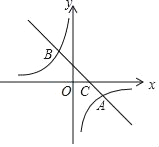
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=
 的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.(1)求k2,n的值;
(2)请直接写出不等式k1x+b<
 的解集;
的解集;(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真阅读下面材料:如果
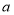 (
(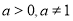 )的b次幂等于N,即有指数式
)的b次幂等于N,即有指数式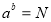 ,那么数b叫做以
,那么数b叫做以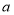 为底N的对数,
为底N的对数,记作:对数式:
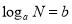
例如:
(1)因为指数式
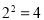 ,所以以2为底,4的对数是2,对数式记作:
,所以以2为底,4的对数是2,对数式记作: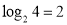
(2)因为指数式
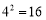 ,所以以4为底,16的对数是2,对数式记作:
,所以以4为底,16的对数是2,对数式记作: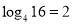
1. 请根据上面阅读材料将下列指数式改为对数试:(1)
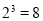 ;(2)
;(2)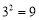
2. 将下列对数式改为指数式:(1)
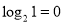 ;(2)
;(2)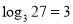
3.计算 :
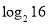
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2018次变换后,等边△ABC的顶点C的坐标为_____.
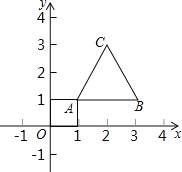
相关试题

