【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2.过点A作对角线BD的平行线与边CD的延长线相交于点E.P为边BD上的一个动点(不与端点B,D重合),连接PA,PE,AC.
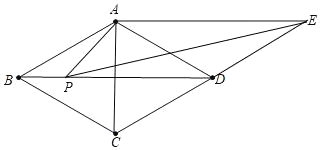
(1)求证:四边形ABDE是平行四边形;
(2)求四边形ABDE的周长和面积;
(3)记△ABP的周长和面积分别为C1和S1,△PDE的周长和面积分别为C2和S2,在点P的运动过程中,试探究下列两个式子的值或范围:①C1+C2,②S1+S2,如果是定值的,请直接写出这个定值;如果不是定值的,请直接写出它的取值范围.
参考答案:
【答案】(1)见解析;(2)ABDE的周长为:![]() ,面积为
,面积为![]() ;
;
(3)①![]() ;②S1+S2的值为定值,这个定值为
;②S1+S2的值为定值,这个定值为![]()
【解析】
(1)利用菱形的性质得:AB∥DE,由两组对边分别平行的四边形可得结论;
(2)设对角线AC与BD相交于点O.根据直角三角形30°角的性质得AC的长,由勾股定理得OB的长和BD的长,根据平行四边形的性质可得其周长和面积;
(3)①先根据三角形的周长计算C1+C2=2AB+BD+AP+PE=4+2![]() +AP+PE,确定AP+PE的最大值和最小值即可;
+AP+PE,确定AP+PE的最大值和最小值即可;
根据轴对称的最短路径问题可得:当P在D处时,AP+PE的值最小,最小值是2+2=4,由图形可知:当P在点B处时,AP+PE的值最大,构建直角三角形计算即可;
②S1+S2的值为定值,这个定值为![]() ,根据面积公式可得结论.
,根据面积公式可得结论.
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
即AB∥DE.
∵BD∥AE,
∴四边形ABDE是平行四边形.
(2)解:设对角线AC与BD相交于点O.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABD=∠CBP=![]() ∠ABC=30°,AC⊥BD.
∠ABC=30°,AC⊥BD.
在Rt△AOB中,AO=![]() AB=1,
AB=1,
∴OB=![]() .
.
∴BD=2BO=2![]() .
.
∴![]() ABDE的周长为:2AB+2BD=4+4
ABDE的周长为:2AB+2BD=4+4![]() ,
,
![]() ABDE的面积为:BDAO=2
ABDE的面积为:BDAO=2![]() ×1=2
×1=2![]() .
.
(3)①∵C1+C2=AB+PB+AP+PD+PE+DE=2AB+BD+AP+PE=4+2![]() +AP+PE,
+AP+PE,
∵C和A关于直线BD对称,
∴当P在D处时,AP+PE的值最小,最小值是2+2=4,
当P在点B处时,AP+PE的值最大,如图2,
过E作EG⊥BD,交BD的延长线于G,
∵∠BDE=150°,
∴∠EDG=30°,
∵DE=2,
∴EG=1,DG=![]() ,
,
Rt△PEG中,BG=2![]() +
+![]() =3
=3![]() ,
,
由勾股定理得:PE=![]() ,
,
∴AP+PE的最大值是:2+2![]() ,
,
∵P为边BD上的一个动点(不与端点B,D重合),
∴4+4+2![]() <C1+C2<4+2
<C1+C2<4+2![]() +2+2
+2+2![]() ,即8+2
,即8+2![]() <C1+C2<6+2
<C1+C2<6+2![]() +2
+2![]() ;
;
(写对一边的范围给一分)
②S1+S2的值为定值,这个定值为![]() ;
;
理由是:S1+S2=![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.
(1)写出点
 的坐标________
的坐标________(2)若P(50,m)在第17段抛物线C17上,则m=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
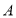 表示的数为
表示的数为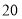 ,点
,点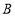 表示的数为
表示的数为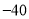 ,动点
,动点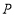 从点
从点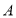 出发以每秒
出发以每秒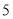 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点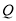 从原点出发以每秒
从原点出发以每秒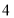 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点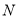 从点
从点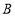 出发以每秒
出发以每秒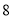 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为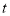 (秒).
(秒). 
(1)点
 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;(2)当
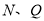 两点重合时,求此时点
两点重合时,求此时点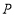 在数轴上所表示的数;
在数轴上所表示的数; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用两个边长分别为a,b的正方形,和两个a×b的长方形,拼成图案(1),图案(1)里含有一个乘法公式,你发现了吗?请写出来: .
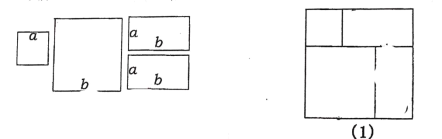
(2)请你用同样的四个图形,再拼出一个图案来,要求也可以说明这个公式,并且同时是对称图形.
(3)现有边长分别为a,b的正方形纸片和长为b、宽为a的长方形纸片各若干张,试选用这些纸片(每种纸片至少用一次)拼成一个长方形,使拼出的长方形面积为
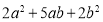 (每两张纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图痕迹)
(每两张纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图痕迹) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,函数
中,函数 的图象与直线
的图象与直线 交于点A(3,m).
交于点A(3,m).(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于
 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

-
科目: 来源: 题型:
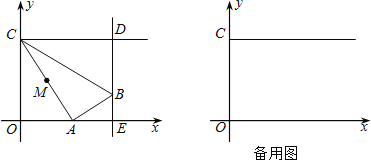
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
(1)当点B与点D重合时,求t的值;
(2)设△BCD的面积为S,当t为何值时,S=
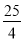 ?
?(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM内部(不包括边),求a的取值范围.
相关试题

