【题目】如图,用两个边长分别为a,b的正方形,和两个a×b的长方形,拼成图案(1),图案(1)里含有一个乘法公式,你发现了吗?请写出来: .
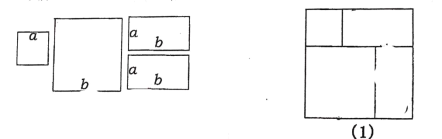
(2)请你用同样的四个图形,再拼出一个图案来,要求也可以说明这个公式,并且同时是对称图形.
(3)现有边长分别为a,b的正方形纸片和长为b、宽为a的长方形纸片各若干张,试选用这些纸片(每种纸片至少用一次)拼成一个长方形,使拼出的长方形面积为![]() (每两张纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图痕迹)
(每两张纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图痕迹)
参考答案:
【答案】(1)![]() ;(2)见详解;(3)见详解
;(2)见详解;(3)见详解
【解析】
(1)求出小正方形与大正方形的面积之和即可发现规律;
(2)由(1)可知四个图形中包含含有一个完全平方公式,根据题意直接画出图形即可;
(3)将2a2+5ab+2b2,因式分解后就可以得到拼成后的矩形的长和宽,按照此长和宽拼成长方形即可.
解:(1)图案(1)的面积=![]() ;
;
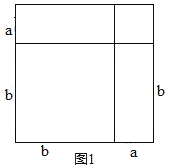
(2)(1)可知四个图形中包含含有一个完全平方公式,根据题意要求拼凑的图形为对称图形,则如图1,即可满足题意
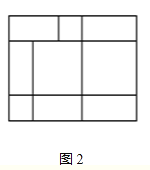
(3)∵2a2+5ab+2b2=(2a+b)(a+2b),a<b,所以矩形的长为a+2b,宽为2a+b,
∴图2所示可满足题意
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
 表示的数为
表示的数为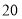 ,点
,点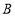 表示的数为
表示的数为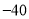 ,动点
,动点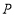 从点
从点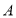 出发以每秒
出发以每秒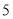 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点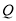 从原点出发以每秒
从原点出发以每秒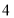 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点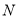 从点
从点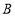 出发以每秒
出发以每秒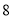 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为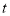 (秒).
(秒). 
(1)点
 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;(2)当
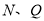 两点重合时,求此时点
两点重合时,求此时点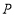 在数轴上所表示的数;
在数轴上所表示的数; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2.过点A作对角线BD的平行线与边CD的延长线相交于点E.P为边BD上的一个动点(不与端点B,D重合),连接PA,PE,AC.
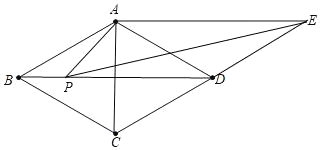
(1)求证:四边形ABDE是平行四边形;
(2)求四边形ABDE的周长和面积;
(3)记△ABP的周长和面积分别为C1和S1,△PDE的周长和面积分别为C2和S2,在点P的运动过程中,试探究下列两个式子的值或范围:①C1+C2,②S1+S2,如果是定值的,请直接写出这个定值;如果不是定值的,请直接写出它的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,函数
中,函数 的图象与直线
的图象与直线 交于点A(3,m).
交于点A(3,m).(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于
 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

-
科目: 来源: 题型:
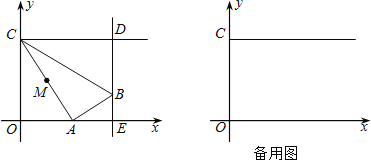
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
(1)当点B与点D重合时,求t的值;
(2)设△BCD的面积为S,当t为何值时,S=
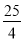 ?
?(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM内部(不包括边),求a的取值范围.
-
科目: 来源: 题型:
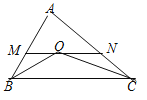
查看答案和解析>>【题目】如图,BO平分∠ABC,CO平分∠ACB,过点O作MN∥BC,分别交AB、AC于点M、N,若AB=12,△AMN的周长为29,则AC= .
相关试题

