【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一把直角三角尺的直角顶点放在点
,将一把直角三角尺的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,其中
的下方,其中![]() .
.

(1)将图1中的三角尺绕点![]() 顺时针旋转至图2,使一边
顺时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中三角尺绕点![]() 按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边
按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边![]() 恰好与射线
恰好与射线![]() 平行;在第 秒时,直线
平行;在第 秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() .
.
(3)将图1中的三角尺绕点![]() 顺时针旋转至图3,使
顺时针旋转至图3,使![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
参考答案:
【答案】(1) 150°;(2) 9或27;6或24 ;(3)见解析.
【解析】
(1)根据角平分线的定义求出∠COM,然后根据∠CON=∠COM+90°解答;(2)分别分两种情况根据平行线的性质和旋转的性质求出旋转角,然后除以旋转速度即可得解;
(3)用∠BOM和∠NOC表示出∠BON,然后列出方程整理即可得解.
解:(1)∵OM平分∠AOC,
∴∠COM=![]() ∠AOC=60°,
∠AOC=60°,
∴∠CON=∠COM+90°=150°;
(2))∵∠AOC=120°,
∴∠BOC=60°,
∵∠OMN=30°,
∴当ON在直线AB上时,MN∥OC,
旋转角为90°或270°,
∵每秒顺时针旋转10°,
∴时间为9或27,
直线ON恰好平分锐角∠BOC时,
旋转角为60°或 180°+60°=240°,
∵每秒顺时针旋转10°,
∴时间为6或24;
故答案为:9或27;6或24.
(3)∵∠MON=90°,∠BOC=60°,
∴∠BON=90°-∠BOM,
∠BON=60°-∠NOC,
∴90°-∠BOM=60°-∠NOC,
∴∠BOM-∠NOC=30°,
故∠BOM与∠NOC之间的数量关系为:∠BOM-∠NOC=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
-
科目: 来源: 题型:
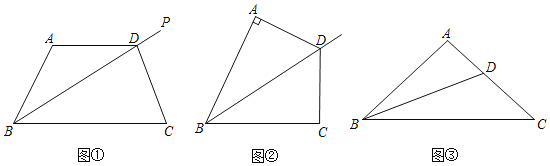
查看答案和解析>>【题目】(问题)如图①,点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD有什么数量关系?
(探究)
探究一:如图②,若∠A=90°,则∠C=180°﹣∠A=90°,即AD⊥AB,CD⊥BC,又因为BD平分∠ABC,所以AD=CD,理由是: .
探究二:若∠A≠90°,请借助图①,探究AD与CD的数量关系并说明理由.
[理论]点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD的数量关系是 .
[拓展]已知:如图③,在△ABC中,AB=AC,∠A=100°,BD平分∠ABC.
求证:BC=AD+BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形
 沿
沿 折叠后点
折叠后点 与
与 重合.若原矩形的长宽之比为
重合.若原矩形的长宽之比为 ,则
,则 的值为( )
的值为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
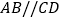 ,点
,点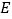 在
在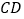 上,点
上,点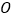 、点
、点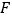 在
在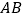 上,
上,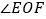 的角平分线
的角平分线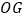 交
交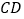 于点
于点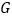 ,过点
,过点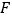 作
作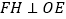 于点
于点 ,己知
,己知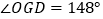 ,则
,则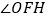 的度数为( )
的度数为( )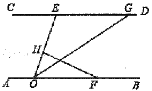
A. 26°B. 32°C. 36°D. 42°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在
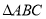 中,若
中,若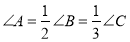 ,则
,则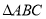 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有
 三点。
三点。(1)连接
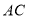 ,若
,若
①线段的长为 (直接写出结果)
②如图1,点
 为
为 轴负半轴上一点,点
轴负半轴上一点,点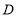 为线段
为线段 上一点,连接
上一点,连接 作
作 ,且
,且 ,当点
,当点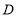 从
从 向
向 运动时,
运动时, 点不变,
点不变, 点随之运动,连接
点随之运动,连接 ,求线段
,求线段 的中点
的中点 的运动路径长;
的运动路径长;(2)如图2,作
 ,连接
,连接 并延长,交
并延长,交 延长线于
延长线于 于
于 .若
.若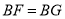 ,且
,且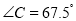 ,在平面内是否存在点
,在平面内是否存在点 ,使以
,使以 为顶点的四边形是平行四边形,若存在,请求出点
为顶点的四边形是平行四边形,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

