【题目】为了迎接元旦,孝昌县政府要在广场上设计一座三角形展台,要求园林工人把它的每条边上摆放上相等盆数的盆栽鲜花(如图所示的每个小圆圈表示一盆鲜花)以美化环境,如果每条边上摆放两盆鲜花,共需要3盆鲜花;如果每条边上摆放3盆鲜花,共需要6盆鲜花;…,按此要求摆放下去:

(1)根据图示填写下表:
每条边上摆放的盆数( | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数( | 3 | 6 | … |
(2)如果要在每条边上摆放![]() 盆鲜花,那么需要鲜花的总盆数 .
盆鲜花,那么需要鲜花的总盆数 .
(3)请你帮园林工人参考一下,能否用2020盆鲜花作出符合要求的摆放?如果能,请计算出每条边上应摆放花的盆数;如果不能,请说明理由.
参考答案:
【答案】(1)9,12,15;(2)S=3n-3 (n是大于2的整数);(3)不能
【解析】
(1)结合图形,发现:每条边上每增加一盆鲜花,总数就增加3盆,依此可得出答案.
(2)结合(1)中的规律即可求出每条边上摆n盆小菊花时需要小菊花的总盆数;
(3)根据题意把2020代入S=3(n-1)中,求出n的值后,即可作出判断.
解:(1)由图知,每条边上每增加一盆鲜花,总数就增加3盆,
故答案为:
每条边上摆放的盆数( | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数( | 3 | 6 | 9 | 12 | 15 | … |
(2)每条边摆两个,则总盆数=3=3(2-1),
每条边摆3个,则总盆数=6=3(3-1),
每条边摆4个,则总盆数=9=3(4-1),
…
每条边摆n个,则总盆数=3(n-1),
∴总盆数=3n-3 (n是大于2的整数)
(3)不能
∵(2020+3)÷3不是整数,
∴不能用2020盆鲜花作出符合要求的摆放.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B. 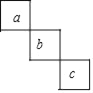 C.
C. 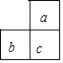 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA为⊙O的切线,A为切点。过A作OP的垂线AB,垂足为点C,交⊙O于点B。延长BO与⊙O交于点D,与PA的延长线交于点E。
(1)求证:PB为⊙O的切线;
(2)试探究线段AD、AB、CP之间的等量关系,并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,作如下探究:
探究一:平移线段OA,使点O落在点B.设点A落在点C,若点B的坐标为(1,2),请在图1中作出BC,点C的坐标是_________;
探究二:将线段OA绕点O逆时针旋转90°,设点A落在点D.则点D的坐标是_______.
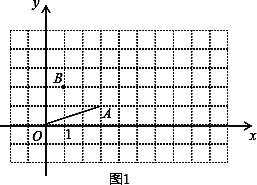
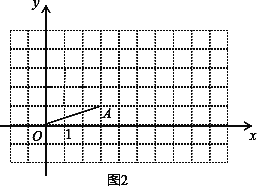
(2) 已知四点O(0,0),A (a,b), C,B(c,d),顺次连结O,A,C,B.
若所得到的四边形是正方形,请直接写出a,b,c,d应满足的关系式是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
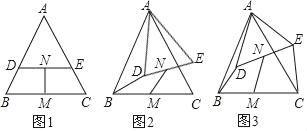
(1)发现:在图1中,
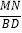 = ;
= ;(2)应用:如图2,将△ADE绕点A旋转,请求出
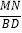 的值;
的值;(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出
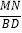 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
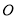 为直线
为直线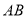 上一点,过点
上一点,过点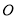 向直线
向直线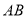 上方引三条射线
上方引三条射线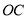 、
、 、
、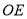 ,且
,且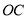 平分
平分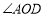 ,
,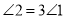 .
.(1)若
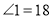 °,求
°,求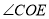 的度数;
的度数;(2)若
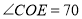 °,求
°,求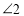 的度数;
的度数;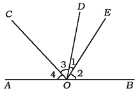
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,能用
 、
、 、
、 三种方法表示同一个角的是( )
三种方法表示同一个角的是( )A.
 B.
B.
C.
 D.
D.
相关试题

