【题目】如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
(1)点A坐标为______;点B坐标为______;点C坐标为______;
(2)画出△ABC关于原点对称的△A1B1C1;
(3)已知M(1,4),在x轴上找一点P,使|PM-PB|的值最大(写出过程,保留作图痕迹),并写出点P的坐标______.

参考答案:
【答案】(1)(﹣1,0),(﹣2,﹣2),(﹣4,﹣1);(2)详见解析;(3)(﹣5,0).
【解析】
(1)根据图象即可写出A、B、C坐标.
(2)根据关于原点对称的定义,画出图形即可.
(3)首先确定点P的位置,然后利用一次函数的性质即可解决问题.
解:(1)于图象可知点A坐标(﹣1,0),点B坐标(﹣2,﹣2),点C坐标(﹣4,﹣1),
故答案为:(﹣1,0),(﹣2,﹣2),(﹣4,﹣1).
(2)△ABC关于原点对称的△A1B1C1如图所示:
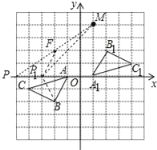
(3)①作点B关于x轴的对称点F(﹣2,2).
②连接MF,由此MF交x轴于P.
点P就是所求的点.
理由:在x轴上任意取一点P1,
∵|P1M﹣P1B|=|P1M﹣P1F|≤FM,
∴当P1与P共点时,|PM﹣PB|的值最大,
设直线FM为y=kx+b,把F、M两点坐标代入得![]() 解得
解得
∴直线FM为![]()
令y=0,得x=﹣5,
∴点P坐标为(﹣5,0).
故答案为(﹣5,0).
-
科目: 来源: 题型:
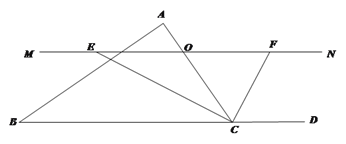
查看答案和解析>>【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, .点
.点 是射线
是射线 上一动点(与点
上一动点(与点 不重合),
不重合), 、
、 分别平分
分别平分 和
和 、分别交射线
、分别交射线 于点
于点 ,
, .
.
(1)①
 的度数是________;
的度数是________;②
 ,
, ________;
________;(2)求
 的度数;
的度数;(3)当点
 运动时,
运动时, 与
与 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=3,BC=9.将矩形纸片折叠,使点B和点D重合.
(1)求ED的长;
(2)求折痕EF的长.

-
科目: 来源: 题型:
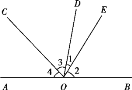
查看答案和解析>>【题目】如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1.
(1)若∠1=18°,求∠COE的度数;
(2)若∠COE=70°,求∠2的度数.
-
科目: 来源: 题型:
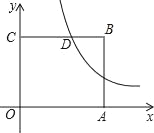
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数
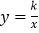 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.(1)求k的值;
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
相关试题

