【题目】已知△ABC中,AB=15,AC=13,AD⊥BC于D,AD=12,⊙O是△ABC的外接圆,则⊙O的半径是 .
参考答案:
【答案】![]()
【解析】解:当△ABC是锐角三角形时,如图,AE是△ABC外接圆的直径.

在Rt△ABD中,BD= ![]() =
= ![]() =9,
=9,
在Rt△ACD中,CD= ![]() =
= ![]() =5,
=5,
∵∠C=∠E,∠ADC=∠ABE=90°,
∴△ADC∽△ABE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() ,
,
∴△ABC的外接圆的半径为 ![]() .
.
当△ABC是钝角三角形时,如图,CE是△ABC的外接圆的直径,作CF⊥AB于F.

∵ ![]() ABCF=
ABCF= ![]() BCAD,
BCAD,
可得CF= ![]() ,
,
由△AEC∽△FBC,可得 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CE= ![]() ,
,
∴△ABC的外接圆的半径为 ![]() ,
,
综上所述,△ABC的外接圆的半径为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用勾股定理的概念和三角形的外接圆与外心对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .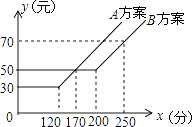
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm.bcm,满足(a-3)2+|2a+b-9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D,设运动时间为t s.
(1)a=______cm,b=______cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
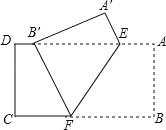
(1)求证:B′E=BF;
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
相关试题

