【题目】已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
参考答案:
【答案】B
【解析】根据题意,本题需分点(1)A为等腰三角形的顶点,点D为等腰三角形底边的中点;(2)点A为等腰三角形底边的中点,点D为等腰三角形的顶点;两种情况来讨论:
(1)如图1,当点A为等腰三角形的顶点,点D为底边的中点时,设BD=DC=a,AB=AC=b,则BE=b-2,CF=b-4,
∵AB=AC,
∴∠B=∠C,
又∵BD=DC,BE≠CF,DE≠DF,
∴点B与点C,点E与点D,点D与点F为对应点,即△BED∽△CDF,
∴BE:CD=BD:CF,即(b-2):a=a(b-4)=3:2,解得:a=![]() ,
,
∴BC=2a=![]() ,该等腰三角形的底边长为:
,该等腰三角形的底边长为: ![]() .
.
 ,
,
(2)如图2,当点D为等腰三角形的顶点,点A为底边中点时,设AB=AC=a,BD=CD=b,则BE=b-3,CF=b-2,
∵BD=CD,
∴∠B=∠C,
∴点B与点C为对应点,
①若点E与点F、点A与点C为对应点,则△BEA∽△CFA,
∴BE:CF=EA:FA=BA:CA,即(b-3):(b-2)=a:a=2:4,此时a、b无解,故此种情况不成立;
②若点E与点A,点A与点F为对应点,由△BEA∽△CAF,
∴BE:CA=EA:AF=BA:CF,即(b-3):a=2:4=a:(b-2),解得:a=![]() ,b=
,b=![]() ,则此时AB=
,则此时AB=![]() ,BE=
,BE=![]() ,
,
又∵AE=2,
∴此时AB、BE、AE不能围成三角形,故此种情况不成立;
综上所述,这个等腰三角形底边长为: ![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形ABC沿着BC方向平移
 cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程
解:过点A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °(用含n的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=
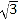
B. BC=1,AC=2,AB=
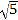
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
相关试题

