【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣ ![]() ,0),且与反比例函数y=
,0),且与反比例函数y= ![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B. 
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
参考答案:
【答案】
(1)解:一次函数y=kx+b(k≠0)的图象过点P(﹣ ![]() ,0)和A(﹣2,1),
,0)和A(﹣2,1),
∴  ,解得
,解得 ![]() ,
,
∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y= ![]() (m≠0)的图象过点A(﹣2,1),
(m≠0)的图象过点A(﹣2,1),
∴ ![]() ,解得m=﹣2,
,解得m=﹣2,
∴反比例函数的解析式为y=﹣ ![]()
(2)解:  ,
,
解得 ![]() ,或
,或  ,
,
∴B( ![]() ,﹣4)
,﹣4)
由图象可知,当﹣2<x<0或x> ![]() 时,一次函数的函数值小于反比例函数的函数值.
时,一次函数的函数值小于反比例函数的函数值.
【解析】(1)根据待定系数法,可得函数解析式;(2)根据二元一次方程组,可得函数图象的交点,根据一次函数图象位于反比例函数图象的下方,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若
 ,则a=b.
,则a=b.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
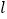 经过原点和点
经过原点和点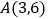 ,点
,点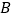 的坐标为
的坐标为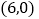 .
.(1)求直线
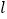 所对应的函数解析式;
所对应的函数解析式;(2)当P在线段OA上时,设
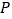 点横坐标为
点横坐标为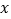 ,三角形
,三角形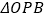 的面积为
的面积为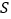 ,写出
,写出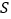 关于
关于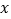 的函数解析式,并指出自变量
的函数解析式,并指出自变量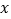 的取值范围;
的取值范围;(3)当P在射线OA上时,在坐标轴上有一点
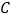 ,使
,使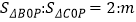 (
(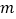 正整数),请直接写出点
正整数),请直接写出点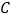 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:



因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
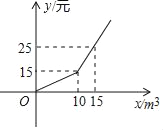
查看答案和解析>>【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y元与每月用水量xm3之间的关系如图所示.
(1)求关于x的函数解析式;
(2)若某用户二、三月份共用水22m3(二月份用水量比三月份用水量多),缴纳水费共35元,则该用户二月份的用水量是多少m3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=
 a,S=
a,S= a2.
a2.(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②求∠ADB的度数.
③若AD=2,BD=4,求△ABC的面积.
(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.
①求∠EAF的度数;
②若CD=5,BD=2,求BC的长.

相关试题

