【题目】抛物线y=ax2+bx+c上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有_______.(填序号)
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
①当x>1时,y随x的增大而减小. ②抛物线的对称轴为直线x=-![]() .
.
③当x=2时,y=-9. ④方程ax2+bx+c=0一个正数解![]() 满足1<
满足1<![]() <2.
<2.
参考答案:
【答案】①④
【解析】
根据二次函数的图象和性质,先取其中几个点坐标求出函数解析式,然后再根据函数作出判断.
![]() 抛物线y=ax2+bx+c
抛物线y=ax2+bx+c
当x=0时,y=3,即c=3
当x=1时,y=3, a+b=0①
当x=-1时,y=-1,a-b+3=-1 ,a-b=-4②
①+②得2a=-4
![]() a=-2 b=2
a=-2 b=2
抛物线解析式为y=-2x2+2x+3
![]() a<0,函数开口向下,当x>1时,y随x的增大而减小,故①对
a<0,函数开口向下,当x>1时,y随x的增大而减小,故①对
对称轴![]() ,故②错
,故②错
当x=2时,y=-1,故③错
-2x2+2x+3=0
![]()
![]() ,故④对
,故④对
![]() ①④
①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,若线段上的个点把这条线段分制为两部分,其中较长的一部分与全长之比等于
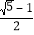 时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.(1)如图1,CD是△ABC的黄金分割线(AD> BD),△ABC的面积为4,求△ACD的面积 ;
(2)如图2,在△ABC中,∠A= 36°,AB=AC=1,过点B作BD平分∠ABC,与AC相交于点D,求证: BD是△ABC的黄金分割线.
(3)如图3,BE、CD是△ABC的黄金分割线(AD> BD,AE> CE),BE、CD相交于点O.
①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由;
②求
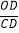 的值.
的值.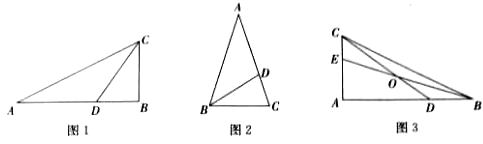
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x+2
x+2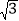 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )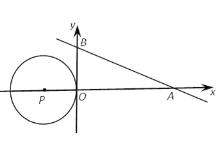
A. 3 B. 4 C. 5 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠A=50°,∠E=45°,则∠F=____°.
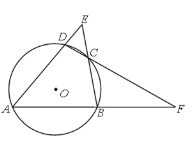
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系中作出函数
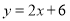 的图象,利用图象解答下列问题:
的图象,利用图象解答下列问题:
(1)求方程
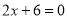 的解:
的解:(2)求不等式
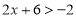 的解集;
的解集;(3)若
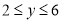 ,求
,求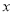 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
相关试题

