【题目】已知:点P(m,4)在反比例函数y=﹣![]() 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)求P、Q两点之间的距离.
参考答案:
【答案】(1)y=-![]() x;(2)15.
x;(2)15.
【解析】
(1)设正比例函数解析式为y=kx(k≠0),把点P的坐标代入反比例函数解析式求出m的值,从而得到点P的坐标,然后代入正比例函数解析式求解即可;
(2)把点Q的坐标代入正比例函数解析式求出n,根据两点间的距离公式即可得到结论.
(1)设正比例函数解析式为y=kx(k≠0),
∵点P(m,4)在反比例函数y=-![]() 的图象上,
的图象上,
∴-![]() =4,
=4,
解得m=-3,
∴P的坐标为(-3,4),
∵正比例函数图象经过点P,
∴-3k=4,
解得k=-![]() ,
,
∴正比例函数的解析式为y=-![]() x;
x;
(2)∵正比例函数图象经过点Q(6,n),
∴n=-![]() ×6=-8,
×6=-8,
∴点Q(6,-8),
∴P、Q两点之间的距离=![]() =15.
=15.
-
科目: 来源: 题型:
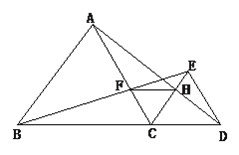
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax﹣a与y=
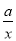 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )A.
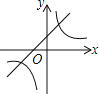 B.
B.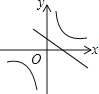
C.
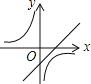 D.
D.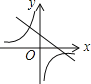
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
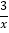 ,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )A. ①④ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
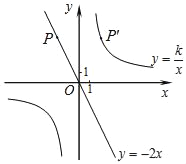
查看答案和解析>>【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=
 (k≠0)的图象上.
(k≠0)的图象上.(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=
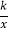 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣
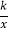 <0的解集(直接写出答案)
<0的解集(直接写出答案)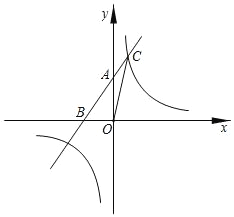
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,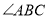 和
和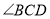 的平分线交于
的平分线交于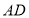 边上一点
边上一点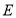 ,且
,且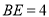 ,
,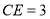 ,则
,则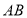 的长是( )
的长是( )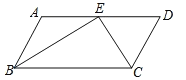
A.3B.4C.5D.2.5
相关试题

