搜索
【题目】为了解某校“阅读工程”的开展情况，区教育局从该校初中生中随机抽取了150名学生进行了阅读情况的调查问卷，并绘制了如图所示不完整的统计图：
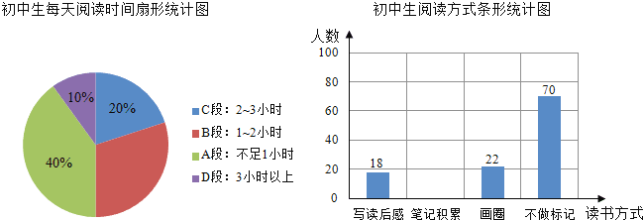
根据上述统计图提供的信息，回答下列问题：
（1）初中生每天阅读时间在哪一段的人数最多？每天阅读时间在B段的扇形的圆心角是多少度?
（2）若将写读后感、笔记积累、画圈点读三种方式称为有记忆阅读，求笔记积累人数占有记忆阅读人数的百分比，并补全条形统计图.
参考答案：
【答案】（1）初中生每天阅读时间不足1小时的人数最多；每天阅读时间在B段的扇形的圆心角是108°；（2）笔记积累人数占有记忆阅读人数的百分比为50%，补全条形统计图见解析.
【解析】
（1）根据扇形统计图得出每天阅读时间在不足1小时的人数最多；由总学生数减去其中的求出笔记积累的学生数，求出B段占的百分比，乘以360°即可得到结果；
（2）求出笔记积累占写读后感、笔记积累、画圈点读三种方式总人数的百分比，补全条形统计图即可．
解：（1）根据扇形统计图得：初中生每天阅读时间不足1小时的人数最多；
阅读时间在B段的扇形圆心角为（1-10%-20%-40%）×360°=108°；
（2）根据题意得：150-（18+22+70）=40（人），笔记积累学生有40人，
根据题意得：
×100%=50%，
则笔记积累人数占有记忆阅读人数的百分比为50%.
补全条形统计图，如图所示．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P是⊙O 外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．
(1)求证：PC是⊙O的切线；
(2)若PD=cm，AC=8cm，求图中阴影部分的面积；
(3)在(2)的条件下，若点E是
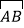的中点，连接CE，求CE的长．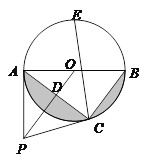
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线
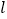的表达式为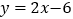
，点A，B的坐标分别为（1，0），（0，2），直线AB与直线
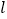相交于点P．（1）求直线AB的表达式；
（2）求点P的坐标；
（3）若直线
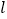上存在一点C，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．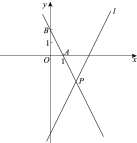
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为： ．
②BC，CD，CF之间的数量关系为： ；（将结论直接写在横线上）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2
，CD=
BC，请求出GE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】国家环保局统一规定：空气质量分为5级，当空气污染指数达
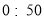为1级，质量为优；
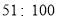时为2 级，质量为良；
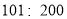时为3级，轻度污染；
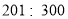时为4级，中度污染；300以上时为5级，重度污染。某城市随机抽取了2019年某些天的空气质量检测结果，并整理绘制成如下两端不完整的统计图。请根据图中信息，解答下列各题。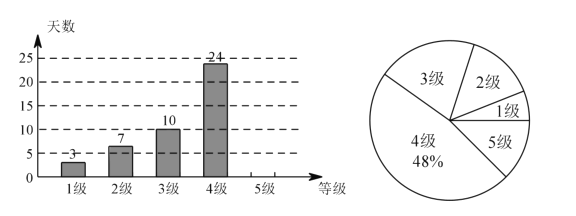
（1）本次调查共抽取了________天的空气质量检测结果进行统计。
（2）补全条形统计图。
（3）扇形统计图中3级空气质量所对应的圆心角为______度。
（4）如果空气污染达到中度污染或者以上，将不适宜进行户外活动，根据目前的统计，请你估计2019年该城市有多少天不适宜开展户外活动。（2019年，共365天）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠AOB＝50°，过点O引射线OC，若∠AOC：∠BOC＝2：3，OD平分∠AOB，求∠COD的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】把几个不同的数用大括号围起来，中间用逗号断开，如：{3，4}，{－3，6，8，18}，我们称之为集合，其中大括号内的数称其为集合的元素，如果一个集合满足：只要其中有一个元素a，使得－2a＋4也是这个集合的元素，这样的集合我们称为条件集合，例如：集合{3，2}，因为－2×3＋4＝－2，－2恰好是这个集合的元素，所以{3，－2}是条件集合：例如：集合{－2，9，8}，因为－2×(－2)＋4＝8，8恰好是这个集合的元素，所以{－2，9，8}是条件集合．
（1）集合{－4，12}______条件集合；集合{
，－
，
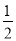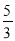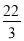}______条件集合 (填“是”或“不是”）（2）若集合{8，10，n}是条件集合，求n的所有可能值．
相关试题
