【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
参考答案:
【答案】(1)是;是;(2)n的可能值有-12,-16,-2,-3,![]() .
.
【解析】
(1)依据一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,即可得到结论;
(2)分情况讨论:若n=-2×8+4,则n=-12;若n=-2×10+4,则n=-16;若-2n+4=8,则n=-2;若-2n+4=10,则n=-3;若-2n+4=n,则n=![]() .
.
解:(1)∵-4×(-2)+4=12,
∴集合{-4,12}是条件集合;
∵![]() ×(-2)+4=
×(-2)+4=![]() ,
,
∴集合{![]() ,-
,-![]() ,
,![]() }是条件集合.
}是条件集合.
故答案为:是;是;
(2)∵集合{8,10,n}是条件集合,
∴若n=-2×8+4,则n=-12;
若n=-2×10+4,则n=-16;
若-2n+4=8,则n=-2;
若-2n+4=10,则n=-3;
若-2n+4=n,则n=![]() ;
;
∴可得n的可能值有-12,-16,-2,-3,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校“阅读工程”的开展情况,区教育局从该校初中生中随机抽取了150名学生进行了阅读情况的调查问卷,并绘制了如图所示不完整的统计图:
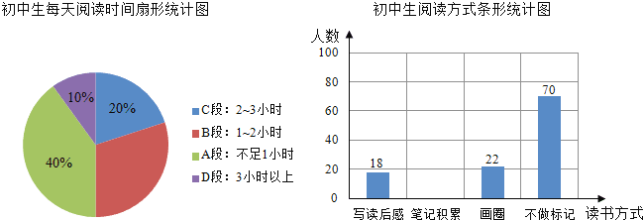
根据上述统计图提供的信息,回答下列问题:
(1)初中生每天阅读时间在哪一段的人数最多?每天阅读时间在B段的扇形的圆心角是多少度?
(2)若将写读后感、笔记积累、画圈点读三种方式称为有记忆阅读,求笔记积累人数占有记忆阅读人数的百分比,并补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定:空气质量分为5级,当空气污染指数达
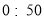 为1级,质量为优;
为1级,质量为优;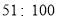 时为2 级,质量为良;
时为2 级,质量为良;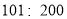 时为3级,轻度污染;
时为3级,轻度污染;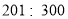 时为4级,中度污染;300以上时为5级,重度污染。某城市随机抽取了2019年某些天的空气质量检测结果,并整理绘制成如下两端不完整的统计图。请根据图中信息,解答下列各题。
时为4级,中度污染;300以上时为5级,重度污染。某城市随机抽取了2019年某些天的空气质量检测结果,并整理绘制成如下两端不完整的统计图。请根据图中信息,解答下列各题。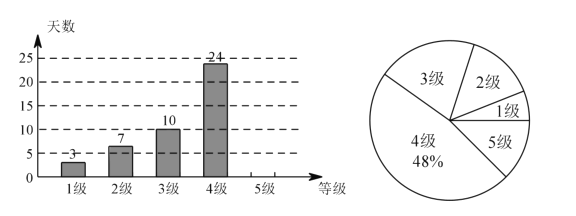
(1)本次调查共抽取了________天的空气质量检测结果进行统计。
(2)补全条形统计图。
(3)扇形统计图中3级空气质量所对应的圆心角为______度。
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2019年该城市有多少天不适宜开展户外活动。(2019年,共365天)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.
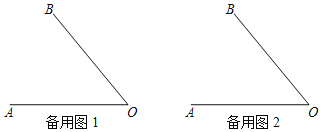
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 的图象与二次函数
的图象与二次函数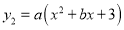 (
(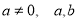 为常数)的图象交于
为常数)的图象交于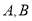 两点,且点
两点,且点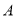 的坐标为
的坐标为 .
.(1)求出
 的值及点
的值及点 的坐标;
的坐标;(2)设
 ,若
,若 时,
时, 随着
随着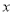 的增大而增大,且
的增大而增大,且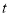 也随着
也随着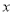 的增大而增大,求
的增大而增大,求 的最小值和
的最小值和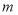 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店试销一款成本为 50 元的排球,规定试销期间单价不低于成本价,且获利不得高于 40%。经试销发现,销售量
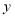 (个)与销售单价
(个)与销售单价 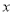 (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.(1)试确定
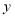 与
与 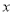 之间的函数关系式;
之间的函数关系式;(2)若该体育用品商店试销的这款排球所获得的利润为
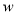 元,试写出利润
元,试写出利润 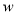 (元)与销售单价
(元)与销售单价 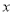 (元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?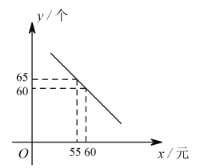
-
科目: 来源: 题型:
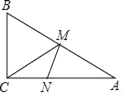
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为_____.
相关试题

