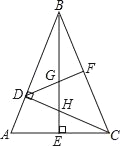
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)求证:BG2﹣GE2=EA2.
参考答案:
【答案】(1)(2)证明详见解析.
【解析】
试题(1)根据三角形的内角和定理求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△DBH≌△DCA即可.(2)根据DB=DC和F为BC中点,得出DF垂直平分BC,推出BG=CG,根据BE⊥AC和∠ABE=∠CBE得出AE=CE,在Rt△CGE中,由勾股定理即可推出答案.
试题解析:(1)∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°,
∴∠BCD=45°=∠ABC,∠A+∠DCA=90°,∠A+∠ABE=90°.
∴DB=DC,∠ABE=∠DCA.
在△DBH和△DCA中,∵∠DBH=∠DCA,BD=CD,∠BDH=∠CDA,
∴△DBH≌△DCA(ASA).∴BH=AC.
(2)连接CG,
∵F为BC的中点,DB=DC,∴DF垂直平分BC. ∴BG=CG.
∵∠ABE=∠CBE,BE⊥AC,∴∠AEB=∠CEB.
在△ABE和△CBE中,∵∠AEB=∠CEB,BE=BE,∠CBE=∠ABE,
∴△ABE≌△CBE(ASA).∴EC=EA.
在Rt△CGE中,由勾股定理得:CG2﹣GE2=EC2.
∴BG2﹣GE2=EA2.
-
科目: 来源: 题型:
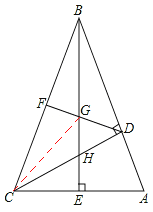
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
-
科目: 来源: 题型:
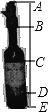
查看答案和解析>>【题目】如图所示的是一种盛装葡萄酒的瓶子,现量得瓶塞AB与标签CD的高度之比为2:3,且瓶子底部DE=
 AB,点C是BD的中点,又量得AE=300mm,设DE的长为
AB,点C是BD的中点,又量得AE=300mm,设DE的长为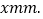
(1)用含
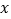 的式于直接表示出AB、BC的长;
的式于直接表示出AB、BC的长;(2)求标签CD的高度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈
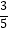 ,tan37°≈
,tan37°≈  ,sin67°≈
,sin67°≈ 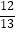 ,tan67°≈
,tan67°≈ 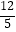 )
)
-
科目: 来源: 题型:
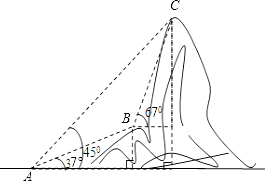
查看答案和解析>>【题目】已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.
(1)如图1:当四边形ABCD是正方形时,且∠EAF=45°,则EF、BE、DF满足的数量关系是 ,请说明理由;
(2)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(1)中的数量关系是否还存在? (填是或否)
(3)在(2)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.
-
科目: 来源: 题型:
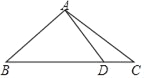
查看答案和解析>>【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

相关试题

