【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

参考答案:
【答案】(1)证明见解析(2)①5或6;②9或10或![]() .
.
【解析】试题分析:(1)设BD=2x,AD=3x,CD=4x,由勾股定理得:AC=5x,AB=5x,AB=AC,从而得到△ABC是等腰三角形;
(2)![]() =40cm2,得到x=2cm,从而得到BD=4cm,AD=6cm,CD=8cm,AC=10cm.分两种情况讨论:
=40cm2,得到x=2cm,从而得到BD=4cm,AD=6cm,CD=8cm,AC=10cm.分两种情况讨论:
①当MN∥BC时,AM=AN;当DN∥BC时,AD=AN,分别求出t的值;
②当点M在BD上,即0≤t<4时,△MDE为钝角三角形,但DM≠DE;
当t=4时,点M运动到点D,不构成三角形;
当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.DE=DM;ED=EM;MD=ME,分别求出t的值.
试题解析:(1)设BD=2x,AD=3x,CD=4x,(x>0)在Rt△ACD中,AC=5x,另AB=5x,AB=AC,∴△ABC是等腰三角形;
(2)![]() =
=![]() ×5x×4x=40cm2,而x>0,∴x=2cm,则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
×5x×4x=40cm2,而x>0,∴x=2cm,则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
①当MN∥BC时,AM=AN,即10-t=t,∴t=5;
当DN∥BC时,AD=AN,有 t=6;
故若△DMN的边与BC平行时,t值为5或6;
②当点M在BD上,即0≤t<4时,△MDE为钝角三角形,但DM≠DE;
当t=4时,点M运动到点D,不构成三角形;
当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t-4=5,∴t=9;
如果ED=EM,则点M运动到点A,∴t=10;
如果MD=ME=t-4,则![]() ,∴t=
,∴t=![]() .
.
综上所述,符合要求的t值为9或10或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a(a-1)-a+1的结果是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长是( )
A. 13 B. 17 C. 22 D. 17或22
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、A做直线l的垂线,垂足分别为点D、E.
(1)问题发现:
①若∠ABC=30°,如图①,则
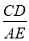 = ;
= ;②∠ABC=45°,如图②,则
 = ;
= ;(2)拓展探究:
当0°<∠ABC<90°,
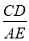 的值有无变化?请仅就图③的情形给出证明.
的值有无变化?请仅就图③的情形给出证明.(3)问题解决:
若直线CE、AB交于点F,
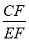 =
= ,CD=4,请直接写出线段BD的长.
,CD=4,请直接写出线段BD的长.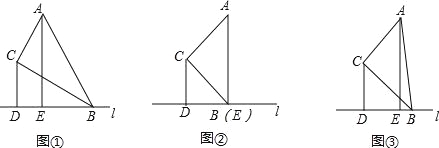
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知1是关于x的方程x2+mx-3=0的一个根,则另一个根为__,m=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】-3的相反数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?
相关试题

