【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)根据∠ACB=∠ECD=90°求出∠DCB=∠ECA,根据SAS推出两三角形全等即可;
(2)根据等腰直角三角形求出∠BAC=∠B=45°,根据全等三角形的性质求出∠EAC=∠B=45°,求出∠EAD=90°,根据勾股定理求出即可.
【解答】(1)证明:∵∠ACB=∠ECD=90°,
∴∠ACB﹣∠ACD=∠ECD﹣∠ACD,
∴∠DCB=∠ECA,
在△ACE和△BCD中

∴△ACE≌△BCD(SAS);
(2)解:∵∠ACB=90°,AC=BC,
∴∠BAC=∠B=45°,
∵△ACE≌△BCD,
∴∠EAC=∠B=45°,
∴∠EAD=90°,
∴在Rt△AED中,∠EAD=90°,AE=3,AD=2,由勾股定理得:ED=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
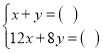 ;乙:
;乙: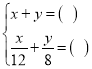 .
.根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示______,y表示_______;
乙:x表示_____,y表示_______.
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)
-
科目: 来源: 题型:
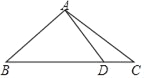
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
-
科目: 来源: 题型:
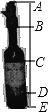
查看答案和解析>>【题目】如图所示的是一种盛装葡萄酒的瓶子,现量得瓶塞AB与标签CD的高度之比为2:3,且瓶子底部DE=
 AB,点C是BD的中点,又量得AE=300mm,设DE的长为
AB,点C是BD的中点,又量得AE=300mm,设DE的长为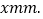
(1)用含
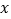 的式于直接表示出AB、BC的长;
的式于直接表示出AB、BC的长;(2)求标签CD的高度。
-
科目: 来源: 题型:
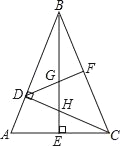
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)求证:BG2﹣GE2=EA2.
-
科目: 来源: 题型:
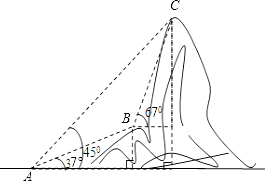
查看答案和解析>>【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈
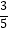 ,tan37°≈
,tan37°≈  ,sin67°≈
,sin67°≈ 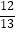 ,tan67°≈
,tan67°≈ 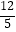 )
)
-
科目: 来源: 题型:
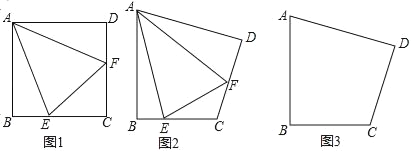
查看答案和解析>>【题目】已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.
(1)如图1:当四边形ABCD是正方形时,且∠EAF=45°,则EF、BE、DF满足的数量关系是 ,请说明理由;
(2)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(1)中的数量关系是否还存在? (填是或否)
(3)在(2)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.
相关试题

