【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论: ①DG=DF; ②四边形EFDG是菱形; ③![]() ;
;
④当![]() 时,BE的长为
时,BE的长为![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
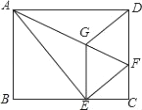
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】试题解析:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正确;
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.故②正确;
如图1所示:连接DE,交AF于点O.
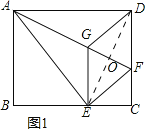
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.故③正确;
GFAF.故③正确;
如图2所示:过点G作GH⊥DC,垂足为H.
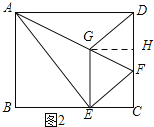
∵EG2=![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2![]() ,
,
∴20=![]() FG(FG+6),整理得:FG2+6FG-40=0.
FG(FG+6),整理得:FG2+6FG-40=0.
解得:FG=4,FG=-10(舍去).
∵DF=GE=2![]() ,AF=10,
,AF=10,
∴AD=![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴![]() ,即
,即![]() .
.
∴GH=![]() .
.
∴BE=AD-GH=4![]() -
-![]() =
=![]() ,故④正确.
,故④正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
 BC,连接CD和EF.
BC,连接CD和EF. 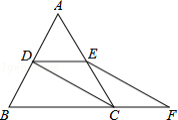
(1)求证:DE=CF;
(2)求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′; B′;C′;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为;
(4)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+4x+k=0有实数根,则k的取值范围是 .
-
科目: 来源: 题型:
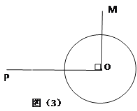
查看答案和解析>>【题目】已知,如图(1),
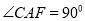 为⊙
为⊙ 的割线,直线
的割线,直线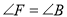 与⊙
与⊙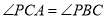 有公共点
有公共点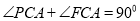 , 且
, 且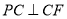 ,
,(1)求证:
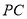 ; 直线
; 直线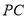 是⊙
是⊙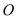 的切线;
的切线;(2)如图(2) , 作弦
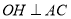 ,使
,使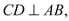 连接AD、BC,若
连接AD、BC,若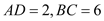 ,求⊙
,求⊙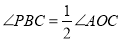 的半径;
的半径;(3)如图(3),若⊙
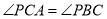 的半径为
的半径为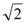 ,
,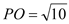 ,
, ,
,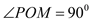 ,⊙
,⊙ 上是否存在一点
上是否存在一点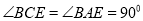 , 使得
, 使得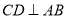 有最小值?若存在,请求出这个最小值;若不存在,说明理由。
有最小值?若存在,请求出这个最小值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
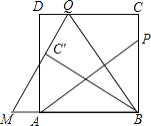
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线互相垂直的四边形
D.对角线相等的四边形
相关试题

