【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
参考答案:
【答案】(1)60,90°;(2)详见解析;(3)300;(4)![]() .
.
【解析】
试题分析:(1)在扇形图中找到“了解很少”所占的百分比,在条形图中找出“了解很少”所对应的人数,据此即可求出接受问卷调查的学生总人数;在条形图中找出“基本了解”部分的人数,用这个人数除以接受调查的总人数所得的商再乘以360°,即可求出扇形统计图中“基本了解”部分所对应扇形的圆心角的度数.(2)先用接受调查总人数-“基本了解”的人数-“基本了解”的人数-“不了解”的人数,算出“了解”的人数,再根据“了解”的人数补全条形统计图.(3)利用总人数900乘以“了解”和“基本了解”所对应的百分比即可求解.(4)首先根据题意列出表格,然后由表格求得所有等可能的结果以及一男一女参加比赛的情况,再利用概率公式即可求得答案.
试题解析:(1)60,90°;
(2) 补全条形统计图如图所示:

(3) 根据题意得:900×![]() =300(人),
=300(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.
(4) 列表法如图所示:
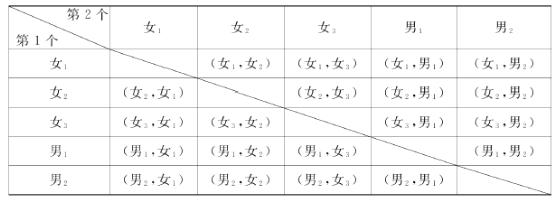
则所有等可能的情况有20种,其中选中1个男生和1个女生的情况有12种,所以恰好抽到1个男生和1个女生的概率:P=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一根直立的旗杆高8m,因刮大风旗杆从点C处折断,顶部B着地且离旗杆底部A4m.
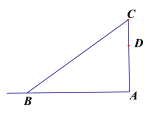
(1)求旗杆距地面多高处折断;
(2)工人在修复的过程中,发现在折断点C的下方1.25m的点D处,有一明显裂痕,若下次大风将旗杆从点D处吹断,则距离旗杆底部周围多大范围内有被砸伤的危险?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC, ∠ABC=90 ,点E在BD上,点F在射线CD上,AE=EF,∠AEF=90 .
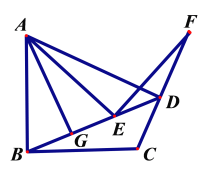
(1)若∠ABE=∠AEB,AG⊥BD,垂足为G,求证:BG=GE.
(2)在(1)的条件下,猜想线段CD与DF的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面文字后,解答问题
有这样一道题目:“已知:二次函数
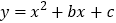 的图象经过点(1,0)_________,
的图象经过点(1,0)_________,求证:这个二次函数图象关于直线
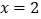 对称”
对称”题目中的横线部分是一段被墨水污染了无法辨认的文字.
根据现有信息,题目中二次函数图象不具有的性质是( )
A. 过点(3,0) B. 顶点是(2,-2)
C. 在X轴上截得的线段长是2 D. 与Y轴交点是(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
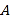 、点
、点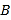 表示的数分别为
表示的数分别为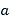 、
、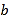 ,则
,则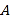 、
、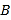 两点之间的距离
两点之间的距离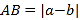 ,线段
,线段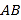 的中点表示的数为
的中点表示的数为 .
.(问题情境)
如图,数轴上点
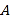 表示的数为
表示的数为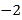 ,点
,点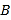 表示的数为8,点
表示的数为8,点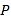 从点
从点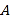 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点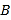 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为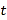 秒(
秒(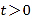 ).
).(综合运用)
(1)填空:
①
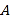 、
、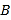 两点之间的距离
两点之间的距离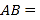 ________,线段
________,线段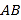 的中点表示的数为__________.
的中点表示的数为__________.②用含
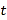 的代数式表示:
的代数式表示: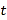 秒后,点
秒后,点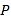 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
 _________时,
_________时,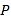 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
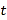 为何值时,
为何值时,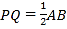 .
.(3)若点
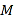 为
为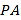 的中点,点
的中点,点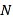 为
为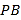 的中点,点
的中点,点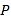 在运动过程中,线段
在运动过程中,线段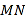 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段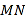 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y
 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校的教室A位于工地O的正西方向,且OA=200米,一部拖拉机从O点出发,以每秒5米的速度沿北偏西53°方向行驶,设拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机的噪声污染范围内,若不在,请说明理由;若在,求出教室A受污染的时间有几秒.(已知:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)

相关试题

