【题目】如图,正方形 ABCD 中,点 G 是边 CD 上一点(不与端点 C,D 重合),以 CG为边在正方形 ABCD 外作正方形 CEFG,且 B、C、E 三点在同一直线上,设正方形 ABCD 和正方形 CEFG 的边长分别为 a 和 b.
(1)分别用含 a,b 的代数式表示图 1 和图 2 中阴影部分的面积 S1、S2;
(2)如果 a+b=5,ab=3,求 S1 的值;
(3)当 S1<S2 时,求![]() 的取值范围.
的取值范围.

参考答案:
【答案】(1)S1= ![]() a2+
a2+ ![]() b2﹣
b2﹣![]() ab, S2=ab﹣
ab, S2=ab﹣![]() b2;(2)8;(3)1<
b2;(2)8;(3)1<![]() <2.
<2.
【解析】(1)利用两个正方形的面积减去空白部分的面积列式即可;
(2)把a+b=5,ab=3,整体代入S1的代数式求得数值即可;
(3)联立不等式,进一步求得答案即可.
(1)S1=a2+b2-![]() a2-
a2-![]() b(a+b)
b(a+b)
=![]() a2+
a2+![]() b2-
b2-![]() ab,
ab,
S2=a(a+b)-b2-![]() a2-
a2-![]() (a-b)(a+b)
(a-b)(a+b)
=ab-![]() b2.
b2.
(2)∵a+b=5,ab=3,
∴S1=![]() a2+
a2+![]() b2-
b2-![]() ab
ab
=![]() (a+b)2-
(a+b)2-![]() ab=
ab=![]() .
.
(3)∵![]() a2+
a2+![]() b2-
b2-![]() ab<ab-
ab<ab-![]() b2.
b2.
∴![]() a2+b2-
a2+b2-![]() ab<0,
ab<0,
∴a2+2b2-3ab<0,
∴(a-2b)(a-b)<0,
∵a>b,
∴a-2b<0,
∴a<2b,
∴1<![]() <2.
<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.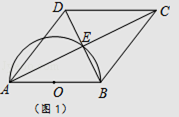
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求扇形AOE的面积.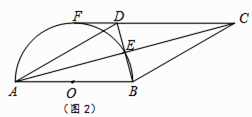
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,∠A=90°,AB=AC=
 +1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
+1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
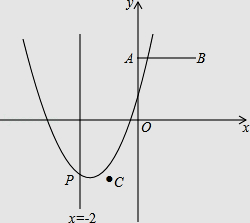
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=7,AC=
 ,∠A=45°,AH⊥HC,垂足为H。
,∠A=45°,AH⊥HC,垂足为H。(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直地公路上有A,B,C三地,,两地相距150km,甲、乙两辆汽车分别从B,C两地同时出发,沿公路匀速相向而行,分别驶往C,B两地.甲、乙两车到A地的距离y1,y2与行驶时间x(h)的函数图象如图2所示.(乙:折线)
(1)请在图1中标出A地的大致位置;
(2)图2中,M点的坐标是_________,该点的实际意义是_________;
(3)求甲车到A地的距离
 与行驶时间
与行驶时间 的函数关系式,直接写出乙车到A地的距离y2与行驶时间
的函数关系式,直接写出乙车到A地的距离y2与行驶时间 的函数关系式,并在图2中补全甲车的函数图象;
的函数关系式,并在图2中补全甲车的函数图象;(4)A地设有指挥中心,指挥中心与两车配有对讲机,两部对讲机在之15km内(含15km)时能够互相通话,直接写出两车可以同时与指挥中心用对讲机通话的时间.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件)
n=50﹣x
销售单价m(元/件)
当1≤x≤20时,m=20+
 x
x当21≤x≤30时,m=10+
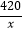
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
相关试题

