搜索
【题目】AB是⊙O的直径，AC、AD是⊙O的两弦，已知AB=16，AC=8，AD=
，求∠DAC的度数．
参考答案：
【答案】（1）30°（2）90°
【解析】试题分析：过O作OE⊥AC于E，OF⊥AD于F，根据垂径定理求出AE、AF，解直角三角形求出∠CAB和∠DAB，即可得出答案．
试题解析：解：过O作OE⊥AC于E，OF⊥AD于F，∵AC=8，AD=8
，∴由垂径定理得：AE=CE=4，AF=DF=4，∵AB=16，∴OA=8，在Rt△AEO中，∠AEO=90°，cos∠CAB=
=
=
，所以∠CAB=60°，在Rt△AFO中，∠AFO=90°，cos∠DAB=
=
=
，所以∠DAB=30°，图1中∠DAC=∠CAB+∠DAB=60°+30°=90°；
图2中∠DAC=∠CAB﹣∠DAB=60°﹣30°=30°；
即∠DAC的度数是90°或30°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，BC＝6，AC＝4．点P、Q分别从点A、B同时出发，点P沿A→C的方向以每秒1个单位长的速度向点C运动，点Q沿B→C的方向以每秒2个单位长的速度向点C运动．当其中一个点先到达点C时，点P、Q停止运动．当四边形ABQP的面积是△ABC面积的一半时，求点P运动的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，由相同边长的小正方形组成的网格图形，A、B、C都在格点上,利用网格画图：（注：所画线条用黑色签字笔描黑）
（1）过点C画AB的平行线CF,标出F点；
（2）过点B画AC的垂线BG，垂足为点G,标出G点；
（3）点B到AC的距离是线段 的长度；
（4）线段BG、AB的大小关系为：BG AB（填“＞”、“＜”或“＝”）,理由是 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系xOy中，直线l经过点O，点A（0，6），经过点A、O、B三点的⊙P与直线l相交于点C（7，7），且CA＝CB.
⑴ 求点B的坐标；
⑵ 如图2，将△AOB绕点B按顺时针方向旋转90°得到△A′O′B.判断直线
与⊙P的位置关系，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，正方形ABCD的顶点坐标分别为 A（1，1），B（1，－1），C（－1，－1），D（－1，1），y轴上有一点 P（0，2）．作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称轴P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此操作下去，则点P2016的坐标为（ ）
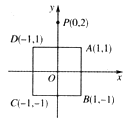
A. （0，2） B. （2，0） C. （0，－2） D. （－2，0）
-
科目： 来源： 题型：
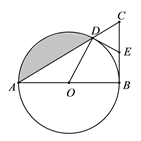
查看答案和解析>>【题目】如图，△ABC中，∠ABC＝90°，以AB为直径的⊙O交AB于点D，点E为BC的中点，连接OD、DE．
⑴ 求证：OD⊥DE．
⑵ 若∠BAC＝30°，AB＝8，求阴影部分的面积．
相关试题
