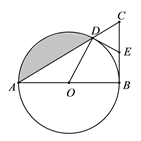
【题目】如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
⑴ 求证:OD⊥DE.
⑵ 若∠BAC=30°,AB=8,求阴影部分的面积.
参考答案:
【答案】![]()
【解析】试题分析:(1)连接BD,易得BDC是直角三角形,E是中点,所以DE=BE,∠CBD=∠EDB,通过倒角知.
(2)用扇形面积减去三角形OAD面积就是阴影部分的面积,其中∠AOD是120°.
试题解析:
⑴ 连接DB.
∵ AB是⊙O的直径 ,
∴ ∠ADB=90°,
∴ ∠CDB=90°,
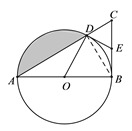
∵ 点E是BC的中点, ∴ DE=CE=![]() ,
,
∴ ∠EDC=∠C,
∵ OA=OD,∴ ∠A=∠ADO,
∵ ∠ABC=90°, ∠A+∠C=90° ,
∴ ∠ADO+∠EDC=90°,
∴ ∠ODE=90°,
∴ OD⊥DE.
⑵∵∠BAC=30°,![]() ∠AOD=120°,
∠AOD=120°,
![]()
![]() cm2,
cm2,
∵AB=8,AO=4, ![]() 勾股定理知AD=4
勾股定理知AD=4![]() ,O到AD的距离是2,
,O到AD的距离是2,
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=
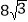 ,求∠DAC的度数.
,求∠DAC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
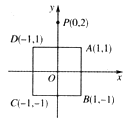
A. (0,2) B. (2,0) C. (0,-2) D. (-2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.
 B.
B.  C.
C.  D.
D. 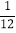
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.

⑴ 求证:AB=AC.
⑵ 若BD=11,DE=2,求CD的长.
相关试题

