【题目】如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.

参考答案:
【答案】3
【解析】
首先根据勾股定理求出BC=3,然后由平行线的性质和角平分线的定义可得∠OBC=![]() ∠ABC,∠ABC=∠OMC,根据三角形外角的性质可得∠OMC=∠OBC+∠MOB,即可证明∠OBC=∠MOB,得到OM=MB,同理可得ON=NC,进而可得△OMN的周长就是BC的长.
∠ABC,∠ABC=∠OMC,根据三角形外角的性质可得∠OMC=∠OBC+∠MOB,即可证明∠OBC=∠MOB,得到OM=MB,同理可得ON=NC,进而可得△OMN的周长就是BC的长.
解:∵∠ACB=90°,AB=5,AC=4,
∴![]() ,
,
∵BO平分∠ABC,OM∥AB,
∴∠OBC=![]() ∠ABC,∠ABC=∠OMC,
∠ABC,∠ABC=∠OMC,
又∵∠OMC=∠OBC+∠MOB,
∴∠OBC=∠MOB,
∴OM=MB,
同理可得ON=NC,
∴△OMN的周长=ON+NM+OM=NC+NM+MB=BC=3,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)当∠B=28°时,求∠AEC的度数;
(2)当AC=6,AB=10时,
①求线段BC的长;
②求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在△ABC中,AB,BC,AC三边的长分别为
 ,
, ,
, ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上:________.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别为
 a,
a,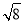 a,
a, a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.探索创新:
(3)若△ABC三边的长分别为
 ,
, ,
, (m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
(m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ADE,BC与DE交于点F.若∠BAE=60°,∠DAC=160°,则∠DFC的度数为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 为常数
为常数 .
.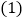 求该二次函数图象与x轴的交点坐标;
求该二次函数图象与x轴的交点坐标; 求该二次函数图象的顶点P的坐标;
求该二次函数图象的顶点P的坐标; 如将该函数的图象向左平移3个单位,再向上平移1个单位,得到函数
如将该函数的图象向左平移3个单位,再向上平移1个单位,得到函数 的图象,直接写出m的值.
的图象,直接写出m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,分别以AC,BC为边长,在三角形外作正方形ACFG和正方形BCED.若AC=4,AB=6,则EF=______.

相关试题

