【题目】问题背景:在△ABC中,AB,BC,AC三边的长分别为![]() ,
,![]() ,
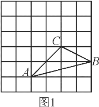
,![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上:________.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别为![]() a,
a,![]() a,
a,![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
(m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
参考答案:
【答案】(1)![]() ;(2)3a2;(3)7mn
;(2)3a2;(3)7mn
【解析】
(1)![]() 的面积
的面积![]() ;
;
(2)![]() 是直角边长为
是直角边长为![]() ,
,![]() 的直角三角形的斜边;
的直角三角形的斜边;![]() 是直角边长为
是直角边长为![]() ,
,![]() 的直角三角形的斜边;
的直角三角形的斜边;![]() 是直角边长为
是直角边长为![]() ,
,![]() 的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为![]() ,
,![]() 的直角三角形的斜边;直角边长为
的直角三角形的斜边;直角边长为![]() ,
,![]() 的直角三角形的斜边;直角边长为
的直角三角形的斜边;直角边长为![]() ,
,![]() 的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解:(1)![]() ;
;
故答案为:![]() ;
;
(2)如图1,在边长为a的正方形网格中,△ABC即为所求作三角形,S△ABC=2a×4a-![]() ×2a×2a-
×2a×2a-![]() ×2a×a-
×2a×a-![]() ×4a×a=3a2
×4a×a=3a2
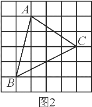
(3)如图2,在每个小长方形的长为m、宽为n的网格中,△ABC即为所求作三角形,其中AB=![]() 、AC=
、AC=![]() 、BC=
、BC=![]() ,S△ABC=4m×4n-
,S△ABC=4m×4n-![]() ×m×4n-
×m×4n-![]() ×3m×2n-
×3m×2n-![]() ×4m×2n=7mn.
×4m×2n=7mn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,
 ,对角线AC平分
,对角线AC平分 .
. 如图1,若
如图1,若 ,
, ,探究AD、AB与对角线AC三者之间的数量关系,写出结论,不必证明.
,探究AD、AB与对角线AC三者之间的数量关系,写出结论,不必证明. 如图2若将
如图2若将 中的条件“
中的条件“ ”去掉,
”去掉, 中的结论是否还成立?并证明你的结论;
中的结论是否还成立?并证明你的结论; 如图3,若
如图3,若 ,试探究AD、AB与对角线AC三者之间的数量关系,写出结论,不必证明.
,试探究AD、AB与对角线AC三者之间的数量关系,写出结论,不必证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)当∠B=28°时,求∠AEC的度数;
(2)当AC=6,AB=10时,
①求线段BC的长;
②求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ADE,BC与DE交于点F.若∠BAE=60°,∠DAC=160°,则∠DFC的度数为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

相关试题

